
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(Ⅰ)88(Ⅱ)当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元
【解析】
试题分析:(Ⅰ)当每辆车的月租金为x元时,租出的车辆![]() (辆),把x=3600代入计算;(Ⅱ)设每辆车的月租金为x元,租赁公司的月收益函数y,建立函数解析式,求出最大值即可
(辆),把x=3600代入计算;(Ⅱ)设每辆车的月租金为x元,租赁公司的月收益函数y,建立函数解析式,求出最大值即可
试题解析:(Ⅰ)当每辆车的月租金定为3600元时,
未租出的车辆数为![]() , ………………2分
, ………………2分
所以这时租出了88辆车.………………3分
(Ⅱ)设每辆车的月租金定为x元,
则租赁公司的月收益为![]() ,…6分
,…6分
整理得![]() .…………9分
.…………9分
所以,当x=4050时,f(x)最大,最大值为f(4050)=307050,………11分
即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.…………12分


科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A. 三点确定一个平面 B. 依次首尾相接的四条线段必共面
C. 直线与直线外一点确定一个平面 D. 两条直线确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直三棱柱![]() 的底面为正三角形,
的底面为正三角形,![]() 分别是
分别是![]() 的中点.
的中点.
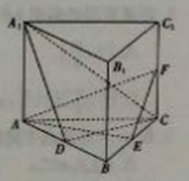
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,
中点,![]() 且
且![]() ,设三棱锥
,设三棱锥![]() 的体积为
的体积为![]() ,三棱锥
,三棱锥![]() 与三棱锥
与三棱锥![]() 的公共部分的体积为
的公共部分的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
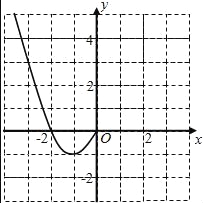
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,BC=CC1,AB⊥BC.点M,N分别是CC1,B1C的中点,G是棱AB上的动点.
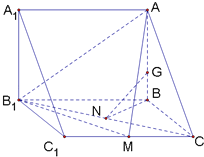
(1)求证:B1C⊥平面BNG;
(2)若CG∥平面AB1M,试确定G点的位置,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com