
| A. | 1 | B. | 5 | C. | $\frac{14}{7}$ | D. | $\frac{16}{7}$ |
分析 先解不等式x2-2x-8≤0的整数解的集合S,再由随机变量ξ=m2,求出分布列,用公式求出期望.
解答 解:由x2-2x-8≤0得-2≤x≤4,符合条件的整数解的集合S={-2,-1,0,1,2,3,4}
∵ξ=m2,故变量可取的值分别为0,1,4,9,16,
相应的概率分别为$\frac{1}{7}$,$\frac{2}{7}$,$\frac{2}{7}$,$\frac{1}{7}$,$\frac{1}{7}$
∴ξ的数学期望Eξ=0×$\frac{1}{7}$+1×$\frac{2}{7}$+4×$\frac{2}{7}$+9×$\frac{1}{7}$+16×$\frac{1}{7}$=5.
故选:B.
点评 本题的考点是离散型随机变量的期望与方差,主要考查随机变量的期望与方差,解题的关键是理解所研究的事件类型确定求概率的方法,有公式求出概率.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
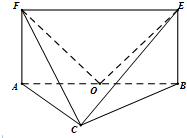 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,DF⊥OE.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,DF⊥OE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 气温x | 14 | 12 | 8 | 6 |
| 用电量y | 22 | 26 | 34 | 38 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=30,p=\frac{1}{10}$ | B. | $a=30,p=\frac{1}{5}$ | C. | $a=15,p=\frac{1}{10}$ | D. | $a=15,p=\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com