
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 令f(x)=$\sqrt{{x}^{2}+2}$-lnx,定义域为(0,+∞),利用导数研究其单调性极值与最值,画出图象.
解答 解:令f(x)=$\sqrt{{x}^{2}+2}$-lnx,定义域为(0,+∞)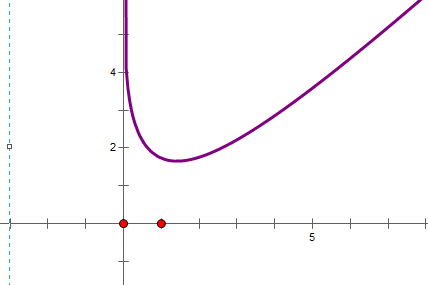 ,
,
令f′(x)=$\frac{x}{\sqrt{{x}^{2}+2}}-\frac{1}{x}$=0,
得x=$\sqrt{2}$,
当0<x<$\sqrt{2}$时,f′(x)<0,
当x>$\sqrt{2}$时,f′(x)>0.
∴$f(\sqrt{2})$是f(x)定义域(0,+∞)内唯一的极值,且是极小值,
故$f(\sqrt{2})$是f(x)的最小值,如图所示.
f($\sqrt{2}$)=2-ln$\sqrt{2}$.
∵$1<\sqrt{2}<e$,
∴$0<ln\sqrt{2}<1$,
∴$1<f(\sqrt{2})<2$
分类讨论:
(m,n)∈{(0,0),(0,2),(0,3),(2,0),(2,2),(2,3),(3,0),(3,2),(3,3)}.
经过验证:只有(0,0)不满足条件.
∴集合D={(m,n)|A∩B≠∅}中的元素有8个.
故选:D.
点评 本题考查了利用导数研究函数的单调性极值与最值、集合的运算性质,考查了数形结合方法、推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{14}{7}$ | D. | $\frac{16}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-1-(1-ln2)e${\;}^{-\frac{1}{2}}$ | B. | ln$\frac{e}{2}$-e-1 | C. | ln2-e-1 | D. | (1-ln2)e${\;}^{-\frac{1}{2}}$-e-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥-$\frac{1}{2}$ | B. | a>0 | C. | -$\frac{1}{2}$<a<0 | D. | -$\frac{1}{2}$<a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 16 | C. | 30 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{7}$ | B. | $\frac{8}{3}$ | C. | -$\frac{8}{3}$ | D. | -$\frac{24}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com