
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
���� ��1����a=0��b=0��c��0ʱ����������
��2����a=0ʱ������Բ�������
��3�����ݲ���ʽ�����ʣ���Ϸ�ʽ����ʽ�����ʽ����ж�
��4������б�ʽ����0����ϲ���ʽ�����ʽ����жϣ�
��� �⣺��1����a=0��b=0��c��0ʱ������b2-4ac��0������ʱax2+bx+c��0��������
��a��b��c��R����ax2+bx+c��0���ij�������ǡ�b2-4ac��0������
��2����ab2��cb2����b��0����ʱa��c������Ҫ�Գ�����
��a��c����b=0ʱ������ʽab2��cb2�������������Բ��������ʼ���ab2��cb2���ij�Ҫ�����ǡ�a��c������
��3����x��y��R������ax��ay��0��a��1������x��y����x=1��y=-1ʱ����������x��y����$\frac{1}{{x}^{2}+1}$��$\frac{1}{{y}^{2}+1}$��������
��4����m��1�����б�ʽ��=4��m+1��2-4m��m+3��=4-4m��0��
��mx2-2��m+1��x+m+3��0�������������ʽ�Ľ⼯ΪR���ʣ�4����ȷ��
����ȷ���ǣ�4����
��ѡ��B��
���� ������Ҫ�������������жϣ��漰����ʽ�����ʣ��ѶȲ���


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
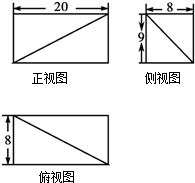
| A�� | 720 | B�� | 960 | C�� | 1200 | D�� | 1440 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 5 | C�� | $\frac{14}{7}$ | D�� | $\frac{16}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
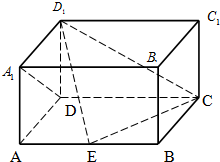 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�AD=AA1=1��AB=2����E����AB���ƶ���
��ͼ���ڳ�����ABCD-A1B1C1D1�У�AD=AA1=1��AB=2����E����AB���ƶ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������S-ABCD�У�����ABCD��ֱ�����Σ�����SA�͵���ABCD����SA=AB=BC=2��AD=1��
��ͼ��������S-ABCD�У�����ABCD��ֱ�����Σ�����SA�͵���ABCD����SA=AB=BC=2��AD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e-1-��1-ln2��e${\;}^{-\frac{1}{2}}$ | B�� | ln$\frac{e}{2}$-e-1 | C�� | ln2-e-1 | D�� | ��1-ln2��e${\;}^{-\frac{1}{2}}$-e-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com