
分析 通过题意可知等腰三角形△F1F2P以F1F2为一腰,结合以椭圆焦点为圆心半径为2c的圆与椭圆位置关系的判断,建立关于a、c的不等式,解之即可得到椭圆C的离心率的取值范围.
解答 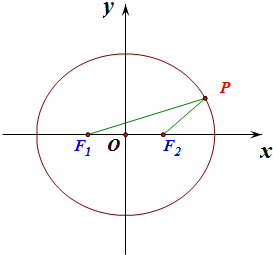 解:根据题意可知等腰三角形△PF1F2中的钝角只能是顶角,
解:根据题意可知等腰三角形△PF1F2中的钝角只能是顶角,
又∵P是椭圆上异于顶点的动点,
∴只能是PF1或PF2为等腰三角形的底边,
下面只考虑以F1P作为等腰三角形的底边这种情况,
由对称性可知另一种情况,此时F1F2=F2P,
∴点P在以F2为圆心,半径为焦距2c的圆上,
∴当以F2为圆心,半径为2c的圆与椭圆C有2个交点时,
存在2个满足条件的等腰△F1F2P,
此时2a-2c<2c+2c,解得a<3c,
所以离心率e>$\frac{1}{3}$,
又∠F1F2P为钝角,∴$|{F}_{1}P{|}^{2}$>$|{F}_{1}{F}_{2}{|}^{2}$+$|{F}_{2}P{|}^{2}$,
∴(2a-2c)2>(2c)2×2,即e<$\sqrt{2}-1$.
这样,总共有4个不同的点P满足题意,
综上所述,离心率的取值范围是:e∈($\frac{1}{3}$,$\sqrt{2}-1$),
故答案为:($\frac{1}{3}$,$\sqrt{2}-1$).
点评 本题考查椭圆的基本性质,考查求椭圆离心率e的取值范围,着重考查了椭圆的标准方程和简单几何性质等知识,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
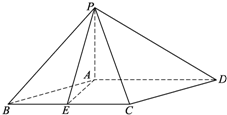 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 范围相同 | B. | 顶点坐标相同 | C. | 焦点坐标相同 | D. | 离心率相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com