
分析 (1)已知等式左边被开方数利用二倍角的余弦函数公式化简,再利用二次根式的性质变形,把A+C的度数代入求出cos(A-C)的值,确定出A-C的度数,即可求出A的度数;
(2)根据(1)确定出A,B,C的度数,连接AO并延长,与圆交于点M,连接MC,过A作AN⊥BC,在直角三角形ACM中,求出AC的长,进而求出AN,BN,NC的长,即可确定出三角形ABC面积.
解答 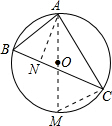 解:(1)∵1+cos2A=2cos2A,1+cos2C=2cos2C,且cosA>0,cosC>0,
解:(1)∵1+cos2A=2cos2A,1+cos2C=2cos2C,且cosA>0,cosC>0,
∴$\sqrt{(1+cos2A)(1+cos2C)}$=2cosAcosC=$\frac{\sqrt{3}-1}{2}$,
即cos(A+C)+cos(C-A)=$\frac{\sqrt{3}-1}{2}$,
∵B=60°,∴A+C=120°①,即cos(A+C)=cos120°=-$\frac{1}{2}$,
∴cos(C-A)=$\frac{\sqrt{3}}{2}$,即C-A=30°②,
联立①②解得:A=45°;
(2)由(1)得:A=45°,B=60°,C=75°,
连接AO并延长,与圆交于点M,连接MC,过A作AN⊥BC,
∴B=M=60°,
在Rt△AMC中,AM=4,
∴AC=2$\sqrt{3}$,
∴AN=NC=$\sqrt{6}$,BN=$\sqrt{2}$,
则S△ABC=$\frac{1}{2}$×($\sqrt{2}$+$\sqrt{6}$)×$\sqrt{6}$=$\sqrt{3}$+3.
点评 此题考查了余弦定理,三角形面积公式,二倍角的余弦函数公式,熟练掌握余弦定理是解本题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
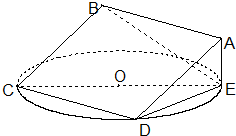 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,A是椭圆C的一
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,A是椭圆C的一查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com