
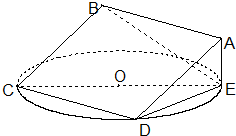
 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.分析 (1)通过证明CD⊥ED,CD⊥AE,然后证明CD⊥平面AED.
(2)所求问题实际是将△ACD(及其内部)绕AE所在直线旋转一周形成一几何体的体积是两圆锥的体积之差.求解即可.
解答 解:(1)证明:因为CE为圆O的直径,所以$∠CDE=\frac{π}{2}$,即CD⊥ED…2分
又因为AE垂直于圆面,CD⊥AE所在平面,所以CD⊥AE…4分
又CD⊥ED,所以CD⊥平面AED…5分
(2)由题意知,将△ACD(及其内部)绕AE所在直线旋转一周形成一几何体的体积是两圆锥的体积之差.
因为异面直线CB与DE所成角为$\frac{π}{6}$,且CB∥DA,所以$∠ADE=\frac{π}{6}$,…7分
又因为AE=1,所以,在Rt△AED中,$DE=\sqrt{3}$,DA=2…9分
在Rt△CDE中,CD=DA=2,$DE=\sqrt{3}$,所以$CE=\sqrt{7}$…10分
所以该几何体的体积$V=\frac{1}{3}π•C{E^2}•AE-\frac{1}{3}π•D{E^2}•AE=\frac{4}{3}π$…12分.
点评 本题考查几何体的体积的求法,直线与平面垂直的判断,考查逻辑推理能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
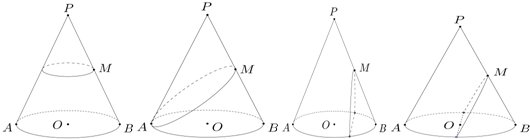
| A. | 1 个 | B. | 2 个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
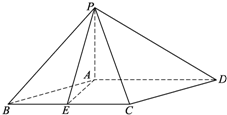 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com