
分析 ①取x=0.5,则[3x]=[1.5]=1,而3[x]=3[0.5]=0,即可判断出正误;
②若m,n∈R,设m=k1+m0,n=k2+n0,k1,k2∈Z,m0,n0∈[0,1),可得[m0-n0]=0或-1,则[m]-[n]=k1-k2,[m-n]=k1-k2+[m0-n0],即可判断出正误;
③由图象即可判断出正误;
④先考虑3个解≥0时,则$\frac{3}{2}≤a<2$;同理可得3个解≤0时,则$\frac{2}{3}<a≤\frac{3}{4}$.即可判断出正误.
解答 解:①取x=0.5,则[3x]=[1.5]=1,而3[x]=3[0.5]=3×0=0,因此不正确;
②若m,n∈R,设m=k1+m0,n=k2+n0,k1,k2∈Z,m0,n0∈[0,1),
(m0-n0)∈(-1,1),∴[m0-n0]=0或-1,则[m]-[n]=k1-k2,[m-n]=[k1-k2+(m0-n0)]=k1-k2+[m0-n0]≤k1-k2,∴[m-n]≤[m]-[n],正确;
③由图象可知:函数f(x)=x-[x]是周期为1的周期函数;
④先考虑3个解≥0时,则$\frac{3}{2}≤a<2$;同理可得3个解≤0时,则$\frac{2}{3}<a≤\frac{3}{4}$.
因此若方程[x]=ax有且仅有3个解,则a∈($\frac{2}{3}$,$\frac{3}{4}$]∪[$\frac{3}{2}$,2),因此不正确.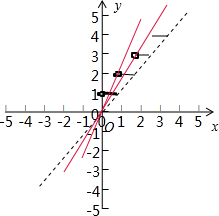
综上可得:只有②③正确.
故答案为:②③.
点评 本题考查了高斯函数的性质、数形结合思想方法、分类讨论思想方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
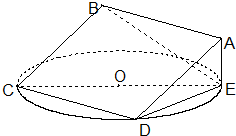 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com