
分析 通过写出前几项猜测通项公式,然后利用数学归纳法证明即可.
解答 解:∵a1=3,(2-an)•an+1=1,
∴an+1=$\frac{1}{2-{a}_{n}}$,
∴a2=$\frac{1}{2-3}$=-1,a3=$\frac{1}{2-(-1)}$=$\frac{1}{3}$,a4=$\frac{1}{2-\frac{1}{3}}$=$\frac{3}{5}$,
…
猜想:数列{an}的通项公式an=$\frac{2n-5}{2n-3}$.
下面用数学归纳法证明:
当n=1时,显然成立;
假设当n=k时,有ak=$\frac{2k-5}{2k-3}$,
∵(2-an)•an+1=1,
∴ak+1=$\frac{1}{2-{a}_{k}}$=$\frac{1}{2-\frac{2k-5}{2k-3}}$=$\frac{1}{\frac{2k-1}{2k-3}}$=$\frac{2k-3}{2k-1}$=$\frac{2(k+1)-5}{2(k+1)-3}$,
即当n=k+1时也成立,
故数列{an}的通项公式an=$\frac{2n-5}{2n-3}$.
点评 本题考查求数列的通项,考查数学归纳法,注意解题方法的积累,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
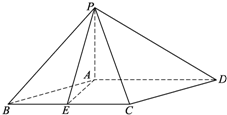 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com