
分析 根据数列的递推关系得到$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n}+1}$,利用裂项法进行求和,即可得到结论.
解答 解:由an+1=an2+an,
得an+1=an(an+1),
取倒数得$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n}+1}$,
则$\frac{1}{{a}_{n}+1}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,
即m=$\frac{1}{{a}_{1}+1}+\frac{1}{{a}_{2}+1}+…+\frac{1}{{a}_{2015}+1}$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{2015}}$-$\frac{1}{{a}_{2016}}$=2-$\frac{1}{{a}_{2016}}$,
∵an+1=an2+an>an,
∴$\frac{1}{{a}_{n+1}}$<$\frac{1}{{a}_{n}}$,
且a3>1,a2016>1.
∴0<$\frac{1}{{a}_{2016}}$<1,
即-1>-$\frac{1}{{a}_{2016}}$>-2,
则2>2-$\frac{1}{{a}_{2016}}$>1,
即1<m<2.
则所求整数部分为1.
故答案为:1.
点评 本题主要考查递推数列的应用.根据递推公式求出$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n}+1}$是解决本题的关键.属于中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)与(1,+∞) | B. | (0,1)∪(1,+∞) | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
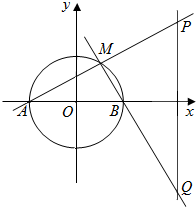 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com