
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
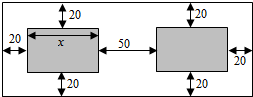 某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.
某单位因工作需要,要制作一批操作台面,台面上有两块大小相同的长方形钢化玻璃(图中阴影部分),每块钢化玻璃的面积为1800cm2,每块钢化玻璃需能放置半径为15cm的圆形器皿,每块钢化玻璃周围与操作台边缘要留20cm空白,两块钢化玻璃的间距为50cm,设钢化玻璃长为xcm,操作台面面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com