Question

16．已知二次函数f（x）=ax²-bx+1，A={x|1≤x≤3}，B={x|1≤x≤4}．若a是从集合A中随机取的一个实数，b是从集合B中随机取的一个实数，求关于x的方程f（x）=0一根在区间$（0\;，\;\frac{1}{2}）$内，另一根在$[0\;，\;\frac{1}{2}]$外的概率．

Answer 1

分析 由题意，本题符合几何概型，只要明确所有实验对应的区域面积以及关于x的方程f（x）=0一根在区间$（0\;，\;\frac{1}{2}）$内，另一根在$[0\;，\;\frac{1}{2}]$外对应区域的面积，利用面积比求概率．

解答 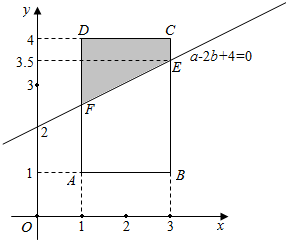解：设事件A为“关于x的方程f（x）=0一根在区间$（0\;，\;\frac{1}{2}）$内，另一根在$[0\;，\;\frac{1}{2}]$外”．…1分
试验的全部结果所构成的区域为Ω={（a，b）|1≤a≤3，1≤b≤4}．…2分
∵f（0）=1＞0…3分∴若满足事件A，须  $f（\frac{1}{2}）＜0$…6分
即 $\frac{1}{4}a-\frac{1}{2}b+1＜0$即a-2b+4＜0              …7分
∴构成事件A的区域为$\left\{\begin{array}{l}{1≤a≤3}\\{1≤b≤4}\\{a-2b+4＜0}\end{array}\right.$　　                   …8分
表示的区域如图所示的阴影部分
其中A（1，1），B）3，1），C（3，4），D（1，4），E（3，3.5），F（1，2.5），
阴影部分的面积为S=$\frac{\frac{1}{2}+\frac{3}{2}}{2}×2$=2        …9分
区域Ω的面积为2×3=6            …10分
∴事件A的概率为$\frac{2}{6}=\frac{1}{3}$                      …11分
∴关于x的方程f（x）=0一根在区间$（0\;，\;\frac{1}{2}）$内，另一根在$[0\;，\;\frac{1}{2}]$外的概率为$\frac{1}{3}$．…12分

点评 本题考查了几何概型概率的求法；关键是明确事件的测度，利用公式解答．