
分析 (1)利用换元法求解函数解析式;
(2)对任意x满足f(3-x)=f(x),说明函数关于x=$\frac{3}{2}$对称,然后直接设出一元二次函数的表达式即可.
解答 解:解:(1)令t=x-2,则x=t+2,t∈R,由已知有
f(t)=3(t+2)-5=3t+1,
故 f(x)=3x+1.
(2)由题知二次函数图象的对称轴为x=$\frac{3}{2}$,又最小值是$\frac{7}{4}$,
则可设f(x)=a(x-$\frac{3}{2}$)2+$\frac{7}{4}$(a≠0),
又图象过点(0,4),则a(0-$\frac{3}{2}$)2+$\frac{7}{4}$=4,解得a=1.
∴f(x)=$(x-\frac{3}{2})^{2}$+$\frac{7}{4}$=x2-3x+4.
所以,f(x)的解析式为:f(x)=x2-3x+4.
点评 本题考查了函数解析式、一元二次函数的基本性质与图形特征,属常考题型.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线CR | B. | 直线BR | C. | 直线AB | D. | 直线BC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,6) | B. | (4,2) | C. | (2,4) | D. | (-4,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
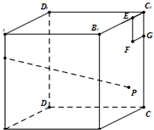 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com