练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．下面有三个命题：
    ①当x＞0时，2x+$\frac{1}{{2}^{x}}$的最小值为2；
    ②将函数y=cos2x的图象向右平移$\frac{π}{6}$个单位，可以得到函数y=sin（2x-$\frac{π}{6}$）的图象；
    ③在Rt△ABC中，AC⊥BC，AC=a，BC=b，则△ABC的外接圆半径r=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$；类比到空间，若三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直，且长度分别为a、b、c，则三棱锥S-ABC的外接球的半径R=$\frac{\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}}{2}$．
    其中错误命题的序号为①②（把你认为错误命题的序号都填上）

    分析 ①根据基本不等式的性质进行判断，
    ②根据三角函数的图象变换关系进行判断，
    ③根据类比推理进行判断．

    解答 解：①当x＞0时，2x+$\frac{1}{{2}^{x}}$$≥2\sqrt{{2}^{x}•\frac{1}{{2}^{x}}}=2$，
    当且仅当2x=$\frac{1}{{2}^{x}}$，即2x=1，x=0，∵x＞0，∴等号取不到，即2x+$\frac{1}{{2}^{x}}$的最小值为2，错误；
    ②将函数y=cos2x的图象向右平移$\frac{π}{6}$个单位，得到y=cos2（x-$\frac{π}{6}$），则可以得到函数y=sin（2x-$\frac{π}{6}$）的图象错误；
    ③直角三角形外接圆半径为斜边长的一半，由类比推理可知若三棱锥的三条侧棱两两互相垂直且长度分别为a，b，c，将三棱锥补成一个长方体，其外接球的半径R为长方体对角线长的一半．故为$\frac{\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}}{2}$．故③正确，
    故答案为：①②

    点评 本题主要考查命题的真假判断，涉及基本不等式的应用，三角函数的图象变换关系以及类比推理，涉及的知识点较多，综合性较强，但难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．判断下列数列哪一个是等差数列（　　）
    A．1，3，6，10，15，21…B．1，2，4，8，16，32，…
    C．1，$\frac{1}{2}$，$\frac{1}{6}$，$\frac{1}{12}$，$\frac{1}{20}$，…D．-3，0，3，6，9，12…

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．“因为四边形ABCD是矩形，所以四边形ABCD的对角线互相平分且相等”，补充以上推理的大前提为矩形的对角线互相平分且相等．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知各项为正的数列{an}的首项为a1=2sinθ（θ为锐角），$\sqrt{4-{a}_{n}^{2}}$+a${\;}_{n+1}^{2}$=2，数列{bn}满足bn=2n+1an．
    （1）求a1，a2，a3，写出an（不用证明）；
    （2）①当x∈（0，$\frac{π}{2}$）时，证明sinx＜x；
    ②若θ=$\frac{π}{4}$，证明a1+a2+…+an＜π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．执行如图所示的程序框图，则输出S的值为（　　）
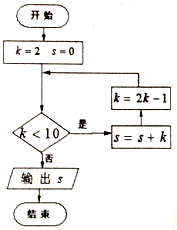
    A．10B．19C．21D．36

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下面几种推理过程是演绎推理的是（　　）
    A．由平面三角形的性质推测空间三棱锥的性质
    B．所有的金属都能够导电，铀是金属，所以铀能够导电
    C．高一参加军训有12个班，1班51人，2班53人，三班52人，由此推测各班都超过50人
    D．在数列{an}中，a1=2，an=2an-1+1（n≥2），由此归纳出{an}的通项公式

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图所示的算法语句中，输出的结果是x=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知数列{an}满足an+1=2an+3•2n，a1=2，则数列{an}的通项公式是（3n-1）•2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知平面内A，B，C，D这4个点中任何3个点都不在一条直线上，写出由其中每3点为顶点的所有三角形．

    查看答案和解析>>

    同步练习册答案