
分析 (Ⅰ)消去参数α得曲线C1的普通方程,将曲线C2化为直角坐标方程,两式作差得直线AB的方程,则直线AB的斜率可求;
(Ⅱ)由C1方程可知曲线是以C1(1,0)为圆心,半径为1的圆,由C2方程可知曲线是以C2(0,2)为圆心,半径为2的圆,又|AB|≤|AC1|+|C1C2|+|BC2|,可知当|AB|取最大值时,圆心C1,C2在直线AB上,进一步求出直线AB(即直线C1C2)的方程,再求出O到直线AB的距离,则△AOB的面积可求.
解答 解:(Ⅰ)消去参数α得曲线C1的普通方程C1:x2+y2-2x=0.…(1)
将曲线C2:ρ=4sinθ化为直角坐标方程得x2+y2-4y=0.…(2)
由(1)-(2)得4y-2x=0,即为直线AB的方程,故直线AB的斜率为$\frac{1}{2}$;
(Ⅱ)由C1:(x-1)2+y2=1知曲线C1是以C1(1,0)为圆心,半径为1的圆,
由C2:x2+(y-2)2=4知曲线C2:是以C2(0,2)为圆心,半径为2的圆.
∵|AB|≤|AC1|+|C1C2|+|BC2|,
∴当|AB|取最大值时,圆心C1,C2在直线AB上,
∴直线AB(即直线C1C2)的方程为:2x+y=2.
∵O到直线AB的距离为$d=\frac{2}{{\sqrt{5}}}=\frac{2}{5}\sqrt{5}$,
又此时|AB|=|C1C2|+1+2=3+$\sqrt{5}$,
∴△AOB的面积为$S=\frac{1}{2}•\frac{2}{5}\sqrt{5}•(3+\sqrt{5})=\frac{{3\sqrt{5}}}{5}+1$.
点评 本题考查了简单曲线的极坐标方程以及参数方程化成普通方程,考查了直线与圆的位置关系,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
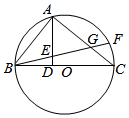 如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.
如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},2}]$ | B. | $({1,\sqrt{2}}]$ | C. | $({\sqrt{2},+∞})$ | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com