练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图在展览厅有一展台，展台是边长为1米的正方体ABCD-A1B1C1D1，面AA1D1D紧靠墙面，一移动光源P在竖直旗杆MN上移动，其中点N在地面上且点N在面BB1C1C上的投影恰好是BC的中点R，MN=3米，NR=2米，设NP=x米，在光源P的照射下，正方体ABCD-A1B1C1D1在面A1B1C1D1紧靠墙面的投影（包括面AA1D1D）的面积为S（x）平方米，则函数y=S（x）的大致图象是（　　）
    A、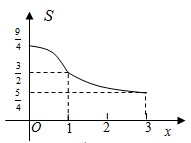
    B、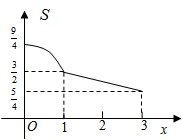
    C、
    D、
    考点：函数的图象
    专题：函数的性质及应用
    分析：利用已知图形，判断正方体的墙面上的投影的变化规律推出结果即可．
    解答： 解由题意可知，P的移动时，正方体的棱长在墙面上的头影是不变的，变化的只是BB1在墙面上的投影的长度，如图：过B1作RU与BB1垂直，交MN于U，墙面于R．显然△B1PU∽△B1RT，RT与PU是线性关系，所以投影面积是一次函数的关系，先大后小，所以D 正确．
    故选：D．
    点评：本题考查函数的图象的判断，一般通过函数的定义域、值域．单调性，奇偶性，变化趋势等知识解答．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知命题p：“若直线ax+y+1=0与直线ax-y+2=0垂直，则a=1”；命题q：“a 
    1
    2
    ＞b 
    1
    2
    是a＞b”的充要条件，则（　　）
    A、p真q假B、p且q真
    C、p或q真D、p或q假

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    按照如图所示的算法框图，则输出的结果是（　　）
    A、1005B、1006
    C、1007D、1008

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    的模为2
    		5
    ，
    b
    =（1，-2），条件p：向量
    a
    的坐标为（4，2），条件q：
    a
    ⊥
    b
    ，则p是q的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充要条件
    D、既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a＞b＞0，a+b=1且x=（
    1
    a
    ）b，y=log (
    1
    a
    +
    1
    b
    )    a，z=log
    1
    b
    a，则x，y，z的大小关系是（　　）
    A、y＜x＜z
    B、z＜y＜x
    C、y＜z＜x
    D、x＜y＜z

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=log 
    1
    2
    cosx，（-
    π
    2
    ＜x＜
    π
    2
    ）的图象大致是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：

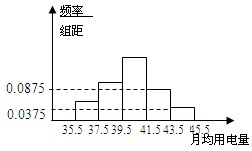    某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如下；其中直方图从左到右前3个小矩形的面积之比为1：2：3．
    （1）该乡镇月均用电量在37.5～39.5之内的居民共有多少户？
    （2）若按分层抽样的方法从中抽出100户作进一步分析，则用电量在37.5～39.5内居民应抽取多少户？
    （3）试根据直方图估算该乡镇居民月均用电量的中位数约是多少？（精确到0.01）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，矩形ABCD所在的平面和平面ABEF互相垂直，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，∠BAF=60°，O，P分别为AB，CB的中点，M为底面△OBF的重心．
    （Ⅰ）求证：PM∥平面AFC；
    （Ⅱ）求直线AC与平面CBF所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

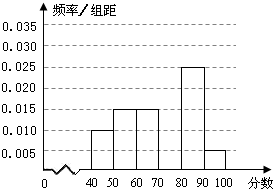    某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题．
    （Ⅰ）求分数在[70，80）内的频率，并补全这个频率分布直方图；
    （Ⅱ）从频率分布直方图中，估计本次考试成绩的中位数；
    （Ⅲ）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．

    查看答案和解析>>

    同步练习册答案