
| a |
| 5 |
| b |
| a |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4-2x |
| A、(1,2) |
| B、(2,3) |
| C、[2,3) |
| D、(1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图在展览厅有一展台,展台是边长为1米的正方体ABCD-A1B1C1D1,面AA1D1D紧靠墙面,一移动光源P在竖直旗杆MN上移动,其中点N在地面上且点N在面BB1C1C上的投影恰好是BC的中点R,MN=3米,NR=2米,设NP=x米,在光源P的照射下,正方体ABCD-A1B1C1D1在面A1B1C1D1紧靠墙面的投影(包括面AA1D1D)的面积为S(x)平方米,则函数y=S(x)的大致图象是( )
如图在展览厅有一展台,展台是边长为1米的正方体ABCD-A1B1C1D1,面AA1D1D紧靠墙面,一移动光源P在竖直旗杆MN上移动,其中点N在地面上且点N在面BB1C1C上的投影恰好是BC的中点R,MN=3米,NR=2米,设NP=x米,在光源P的照射下,正方体ABCD-A1B1C1D1在面A1B1C1D1紧靠墙面的投影(包括面AA1D1D)的面积为S(x)平方米,则函数y=S(x)的大致图象是( )A、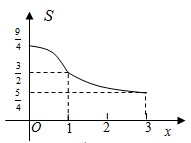 |
B、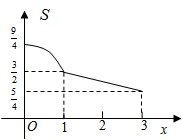 |
C、 |
D、 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| AB |
| 2 |
| OP |
| OA |
| OB |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com