
| A. | (1,$\sqrt{2}$] | B. | (1,$\sqrt{3}$] | C. | [$\frac{\sqrt{5}}{2}$,+∞) | D. | [$\sqrt{3}$,+∞) |
分析 由于△PAB可为正三角形,可得∠OPA=30°,OP=2b≥a,再利用离心率计算公式即可得出.
解答 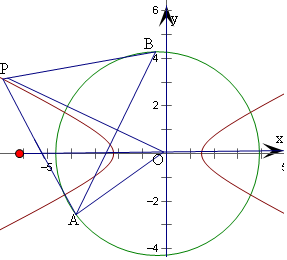 解:∵△PAB可为正三角形,
解:∵△PAB可为正三角形,
∴∠OPA=30°,
∴OP=2b,
则2b≥a,
∴$\frac{b}{a}$≥$\frac{1}{2}$,
∴双曲线C的离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$
≥$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$.
∴双曲线C的离心率的取值范围是[$\frac{\sqrt{5}}{2}$,+∞).
故选:C.
点评 本题考查了双曲线与圆的标准方程及其性质、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
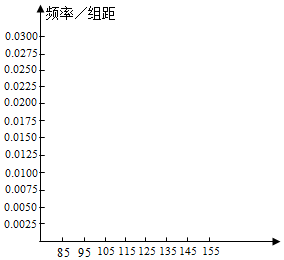 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | 0.025 |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥O-ABC中,平面OAC⊥平面OAB,OC⊥OA,且OA=OB=OC=2,M为△ABC内部一点,点P在OM的延长线上,且OM=$\frac{1}{3}$MP,PA=PB.
如图,三棱锥O-ABC中,平面OAC⊥平面OAB,OC⊥OA,且OA=OB=OC=2,M为△ABC内部一点,点P在OM的延长线上,且OM=$\frac{1}{3}$MP,PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2 | B. | 2:3 | C. | 1:3 | D. | 3:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 不存在 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com