Question

13．高二年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：

分组	频数	频率
[85，95）	①	0.025
[95，105）		0.050
[105，115）		0.200
[115，125）	12	0.300
[125，135）		0.275
[135，145）	4	②
[145，155]		0.050
合计		③

（1）根据图表，①②③处的数值分别为1、0.1、1；
（2）在所给的坐标系中画出[85，155]的频率分布直方图；
（3）根据题中信息估计总体落在[125，155]中的概率．

Answer 1

分析 （1）由频率=$\frac{频数}{总数}$，结合频率分布表能求出结果．
（2）由频率分布表能画出区间[85，155]上的频率分布直方图．
（3）根据题中信息能估计总体落在[125，155]中的概率．

解答 解：（1）∵数学成绩落在区间[115，125）的频数为12，频率为0.300，
∴参与抽查的样本容量为$\frac{12}{0.300}$=40，
由于合计的频率和一定为1，故③应填1；
由数学成绩落在区间[135，145）的频数为4，可得其频率为$\frac{4}{40}$=0.100，故②应填0.1；
由于[85，95）的频率为0.025，∴$\frac{①}{40}=0.025$，解得①处应填1．
故答案为：1，0.1，1．
（2）区间[85，155]上的频率分布直方图如下图所示：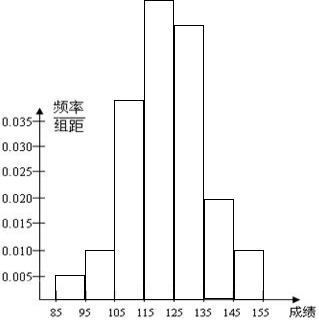

（3）根据题中信息估计总体落在[125，155]中的概率为：
0.275+0.100+0.050=0.425．

点评 本题考查频率分布表、频率分丰直方图的作法，考查概率的求法，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．