
分析 根据向量模长与向量数量积之间的关系进行求解即可.
解答 解:∵|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{13}$,
∴|2$\overrightarrow{a}$-$\overrightarrow{b}$|2=($\sqrt{13}$)2,
即4|$\overrightarrow{a}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$+|$\overrightarrow{b}$|2=13,
即16-4$\overrightarrow{a}$•$\overrightarrow{b}$+9=13,
则$\overrightarrow{a}$•$\overrightarrow{b}$=3,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{3}{2×3}=\frac{1}{2}$,
则<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查向量夹角的计算,根据向量长度和向量数量积的关系进行求解是解决本题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
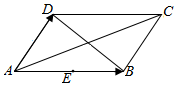
| A. | $\overrightarrow{AC}$=$\overrightarrow a$+$\overrightarrow b$ | B. | $\overrightarrow{BD}$=$\overrightarrow a$-$\overrightarrow b$ | C. | $\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow a$ | D. | $\overrightarrow{CB}$=-$\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
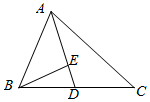 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,D在线段BC上.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,D在线段BC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<3} | B. | {x|-3<x<3} | C. | {0,1,2} | D. | {0,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {(x,y,z)|(x-1)2+y2+z2≤1} | B. | {(x,y,z)|(x-1)2+y2+z2=1} | ||
| C. | {(x,y,z)|(x-1)+y+z≤1} | D. | {(x,y,z)|x2+y2+z2≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 推理形式错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com