Question

3．实数a，b，c，d满足|b-a+2|+（c+d²-3lnd）²=0，则（b-d）²+（a-c）²的最小值是8．

Answer 1

分析 化简可得a=b+2，c=3lnd-d²，从而可得点（b，a）在函数f（x）=x+2的图象上，点（d，c）在函数g（x）=3lnx-x²的图象上；从而问题化为求函数g（x）=3lnx-x²上的点到直线f（x）=x+2的距离的最小值；结合图象求解即可．

解答 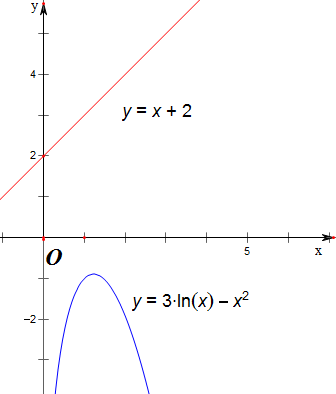解：由题意可知，
b-a+2=0，c+d²-3lnd=0；
故a=b+2，c=3lnd-d²，
即点（b，a）在函数f（x）=x+2的图象上，
点（d，c）在函数g（x）=3lnx-x²的图象上，
故求（b-d）²+（a-c）²的最小值可转化为
求函数g（x）=3lnx-x²上的点到直线f（x）=x+2的距离的最小值；
令g′（x）=$\frac{3}{x}$-2x=1得，x=1；
故点（1，-1）到直线f（x）=x+2的距离最小，
d=$\frac{|1+2-（-1）|}{\sqrt{1+1}}$=2$\sqrt{2}$；
故（b-d）²+（a-c）²的最小值是$（2\sqrt{2}）^{2}$=8；
故答案为：8．

点评 本题考查了导数的综合应用及几何意义的应用，将问题转化为求函数g（x）=3lnx-x²上的点到直线f（x）=x+2的距离的最小值是个难点，属于难题．