
分析 求定积分得到m=6,再利用二项式定理求得展开式中ab2cm-3的系数即可.
解答 解:∵m=3$\int_0^π$sinxdx=-3cosx${|}_{0}^{π}$=6,
∴二项式(a+2b-3c)6 =[(2b-3c)+a]6展开式中含ab2c3的项
为${C}_{6}^{1}$•a•(2b-3c)5;
对于(2b-3c)5,含b2c3的项为${C}_{5}^{3}$•(2b)2•(-3c)3,
故含ab2c3的项的系数为${C}_{6}^{1}$•22•${C}_{5}^{3}$•(-3)3=-6480.
故答案为:-6480.
点评 本题主要考查了定积分的计算与二项式定理的应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 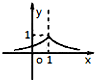 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{n+1}$ | B. | $\frac{2}{n+2}$ | C. | ($\frac{2}{3}$)n | D. | ($\frac{2}{3}$)n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 18 | C. | -15 | D. | -26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},\frac{3}{2}})$ | B. | $[{1,\frac{5}{4}})$ | C. | $({1,\frac{3}{2}})$ | D. | $[{1,\frac{3}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com