
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
分析 (1)由所给数据看出,年需求量与年份之间是近似直线上升,利用配回归直线方程,对数据预处理,求出预处理后的回归直线方程,从而求出对应的回归直线方程;
(2)利用所求的回归直线方程,计算2014年的粮食需求量即可.
解答 解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据预处理如下:
| 年份-2 006 | -4 | -2 | 0 | 2 | 4 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
点评 本题考查了求线性回归方程以及利用回归直线方程预测结果的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
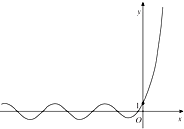 已知如下六个函数:y=x,y=x2,y=lnx,y=2x,y=sinx,y=cosx,从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=2x+sinx.
已知如下六个函数:y=x,y=x2,y=lnx,y=2x,y=sinx,y=cosx,从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=2x+sinx.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
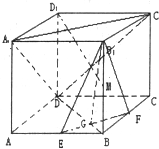 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,EF与BD交于点G,M为棱BB1上一点.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,EF与BD交于点G,M为棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com