
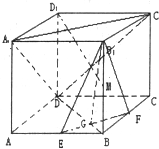
 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,EF与BD交于点G,M为棱BB1上一点.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,EF与BD交于点G,M为棱BB1上一点.分析 (1)根据EF∥AC、AC∥A1C1 证得EF∥A1C1,再利用直线和平面平行的判定定理证得平面 EF∥A1C1D.
(2)当B1M:MB的值为1时,D1M⊥平面 EFB1 .先证明B1E⊥D1M,再证明EF⊥D1M,再结合EF∩B1E=E,从而证得D1M⊥平面 EFB1 .
(3)设点D到平面 EFB1的距离为d,根据${V_{D={B_1}EF}}={V_{{B_1}=DEF}}$,求得d的值.
解答 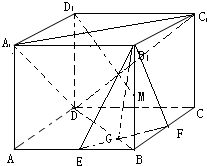 解:(Ⅰ)∵E、F分别是AB、BC的中点,∴EF∥AC,又AC∥A1C1,
解:(Ⅰ)∵E、F分别是AB、BC的中点,∴EF∥AC,又AC∥A1C1,
∴EF∥A1C1,而AC?平面 A1C1D,EF?平面 A1C1D,∴EF∥平面AC1D1.
(II)当B1M:MB=1时,D1M⊥平面EFB1,证明如下:
∵B1M:MB=1,∴A1M⊥B1E.
又A1D1⊥平面AA1BB1,∴A1D1⊥B1E,∴B1E⊥平面A1MD,∴B1E⊥D1M ①.
又EF⊥平面DD1B1B,∴EF⊥D1M ②,又EF∩B1E=E ③,
∴由①②③可得D1M⊥平面EFB1 .
( III)设点D到平面EFB1的距离d,∵${V_{D={B_1}EF}}={V_{{B_1}=DEF}}$,
∴$\frac{1}{3}d•{S_{△{B_1}EF}}=\frac{1}{3}B{B_1}•{S_{△DEF}}$,即 $\frac{1}{3}•d$•($\frac{1}{2}$•EF•B1G )=$\frac{1}{3}$•a•($\frac{1}{2}$•EF•DG),即dB1G=a•DG,
∴d=$\frac{DG}{{B}_{1}G}$•a=a.
点评 本题猪腰考查直线和平面平行的判定与性质,直线和平面垂直的判定与性质,用等体积法求点到平面的距离,属于中档题.


科目:高中数学 来源: 题型:解答题
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 奇函数或偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},\frac{3}{2}})$ | B. | $[{1,\frac{5}{4}})$ | C. | $({1,\frac{3}{2}})$ | D. | $[{1,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{9}=1$ | C. | $\frac{y^2}{18}-\frac{x^2}{18}=1$ | D. | $\frac{x^2}{18}-\frac{y^2}{18}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否需要志愿者 性别 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com