
(本小题满分15分)如图,某公园在一块绿地的中央修建两个相间的矩形池塘,每个面积为10000米 ,池塘前方要留4米宽的走到,其余各为2米宽的走道,问每个池塘的长宽各为多少时占地总面积最少?
,池塘前方要留4米宽的走到,其余各为2米宽的走道,问每个池塘的长宽各为多少时占地总面积最少?

每个池塘的长为100 米,宽为50
米,宽为50 米时占地面积最小.
米时占地面积最小.
【解析】
试题分析:利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:设池塘的长为 米时占地总面积为S(米2)
米时占地总面积为S(米2)
故池塘的宽 米.
米.
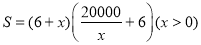
 6分
6分

 (米2) 10分
(米2) 10分
故当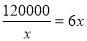
即 (米)
(米)
 (米)时
(米)时
答:每个池塘的长为100 米,宽为50
米,宽为50 米时占地面积最小. 15分
米时占地面积最小. 15分
考点:利用基本不等式解决实际问题


科目:高中数学 来源:2014-2015学年江西省高二上学期第一次月考理科数学试卷(解析版) 题型:解答题
(12分)知直线 与圆O:
与圆O: 相交于A、B二点,且
相交于A、B二点,且 .
.
(1)求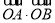 的值.
的值.
(2)若直线AB过点(2,1),求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古赤峰市高二下学期期末理科数学试卷(解析版) 题型:解答题
如图,椭圆C: +
+ =1(a>b>0)的长轴长为4,不过原点O的斜率为﹣
=1(a>b>0)的长轴长为4,不过原点O的斜率为﹣ 的直线l与椭圆C相交于A、B两点,已知点P(2,1)且直线OP平分线段AB.
的直线l与椭圆C相交于A、B两点,已知点P(2,1)且直线OP平分线段AB.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△OAB面积取最大值时直线l的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com