
分析 过点P作PH⊥平面ABC于H,可得∠PAH是直线PA与底面ABC所成的角,得cos∠PAH=$\frac{\sqrt{6}}{3}$.求出PA=PB=PC=$\sqrt{2}$,将三棱锥扩充为正方体,其外接球为三棱锥外接球,正方体的对角线长为$\sqrt{6}$,可得三棱锥外接球的半径,即可求出三棱锥外接球的表面积.
解答 解: 过点P作PH⊥平面ABC于H,则
过点P作PH⊥平面ABC于H,则
∵AH是PA在平面ABC内的射影
∴∠PAH是直线PA与底面ABC所成的角,得cos∠PAH=$\frac{\sqrt{6}}{3}$,
∵△ABC是边长为2等边三角形,
∴AH=$\frac{2\sqrt{3}}{3}$,
∴Rt△PAH中,AH=PA∠PAH,∴PA=$\sqrt{2}$
∴PB=PC=$\sqrt{2}$,∴PA,PB,PC互相垂直,
将三棱锥扩充为正方体,其外接球为三棱锥外接球,正方体的对角线长为$\sqrt{6}$,
∴三棱锥外接球的半径R=$\frac{\sqrt{6}}{2}$,
因此该三棱锥外接球的表面积为S=4πR2=6π.
故答案为:6π.
点评 本题给出三棱锥的三条侧棱两两相等,在已知一条侧棱与底面所成角的情况下求外接球的表面积,着重考查了直线与平面所成角的定义、球内接多面体和球表面积的求法等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5,10,15,20,25 | B. | 2,4,6,8,10 | C. | 1,2,3,4,5 | D. | 7,17,27,37,47 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
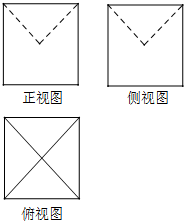 某几何体的三视图如图所示,图中的四边形都是边长为3的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为3的正方形,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{45}{2}$ | B. | $\frac{16}{3}$ | C. | 9-$\frac{π}{6}$ | D. | 27-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 32 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
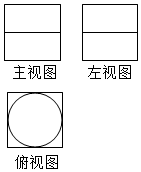 如图所示,一个几何体的主视图和左视图都是边长为4的正方形,中间线段平分正方形,俯视图中有一内切圆,则该几何体的全面积为( )
如图所示,一个几何体的主视图和左视图都是边长为4的正方形,中间线段平分正方形,俯视图中有一内切圆,则该几何体的全面积为( )| A. | 64+8π | B. | 56+12π | C. | 32+8π | D. | 48+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1±\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}±1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1<x<2} | C. | {x|x≥2或x≤-1} | D. | {x|x>2或x<-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com