
| A. | x>5是命题 | |
| B. | 命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” | |
| C. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | |
| D. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
分析 直接由命题的概念判断A;写出特称命题的否定判断B;写出原命题的逆命题,判断真假后判断C;由充分必要条件的判断方法判断D.
解答 解:对于A,x>5没法判断真假,不是命题,A错误;
对于B,命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,B错误;
对于C,命题“在△ABC中,若A>B,则sinA>sinB”的逆命题是“在△ABC中,若sinA>sinB,则A>B”,
若sinA>sinB成立,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=2R$,得a>b,即A>B.
反之,若A>B成立,∴a>b,
∵a=2RsinA,b=2RsinB,∴sinA>sinB,则sinA>sinB是A>B的充要条件,即命题“在△ABC中,若A>B,则sinA>sinB”的逆命题是真命题,C错误;
对于D,若b=0,则f(x)=ax2+c是偶函数,若f(x)=ax2+bx+c是偶函数,则f(-x)-f(x)=0,
即ax2-bx+c-ax2-bx-c=0,∴b=0.
∴“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件.命题D正确.
故选:D.
点评 本题考查命题的真假判断与应用,考查了充分必要条件的判定方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
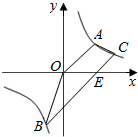 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{|x|}{x}$与 y=1 | B. | y=$\frac{{x}^{3}+x}{{x}^{2}+1}$与y=x | ||
| C. | y=x与y=($\sqrt{x}$)2 | D. | y=|x|与y=$\left\{\begin{array}{l}{x,x>1}\\{-x,x<1}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com