
| A. | a<0 | B. | a≤0 | C. | a≤-$\frac{11}{8}$ | D. | a<-$\frac{11}{8}$ |
分析 由题意可得f(x)在R上为递减函数,运用指数函数和一次函数的单调性,注意分界点x=2,可得2a+2≤($\frac{1}{2}$)2-1,解不等式即可得到所求范围.
解答 解:任意的实数x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,可得
f(x)在R上为递减函数,
显然当x<2时,f(x)=($\frac{1}{2}$)x-1递减;
当x≥2时,f(x)=ax+2,由递减函数,可得a<0,①
由单调性的定义可得2a+2≤($\frac{1}{2}$)2-1,
解得a≤-$\frac{11}{8}$,②
由①②可得a≤-$\frac{11}{8}$,
故选:C.
点评 本题考查分段函数的运用,考查单调性的运用,注意运用单调性的定义,考查指数函数和一次函数的单调性的运用,属于中档题和易错题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{18}$ | C. | $\frac{2}{21}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
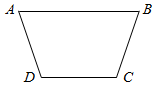 某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-1,1] | C. | [1,+∞) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q是真命题 | B. | ¬p∨q是真命题 | C. | ¬q是假命题 | D. | p∧¬q是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com