
分析 (Ⅰ)先求出函数g(x)的导数,从而求出函数的单调区间;
(Ⅱ)先求出g(x)在x∈($\frac{2}{3}$,+∞)上没有零点,再得到kek<$\frac{2}{3}$且f(ek)≤0即可;
(Ⅲ)通过lnx-x+1≤0在(0,+∞)上恒成立,结合f(n2)≤1-$\frac{1}{{n}^{2}}$,从而得到结论.
解答 解:(Ⅰ)由题意得g(x)的定义域为(0,+∞),
∵g′(x)=$\frac{(3x-2)(x-2)}{4x}$,
∴g(x)在(0,$\frac{2}{3}$),(2,+∞)递增,在($\frac{2}{3}$,2)递减;
(Ⅱ)∵g(x)在x∈($\frac{2}{3}$,+∞)上的最小值为g(2),
且g(2)=$\frac{3}{8}$×22-4+2+ln2=ln2-$\frac{1}{2}$=$\frac{ln4-1}{2}$>0,
故g(x)在x∈($\frac{2}{3}$,+∞)上没有零点,
从而,要使函数g(x)在[ek,+∞),(k∈z)上有零点,
并考虑到g(x)在(0,$\frac{2}{3}$)上单调递增,且在($\frac{2}{3}$,2)上单调递减,
故只需kek<$\frac{2}{3}$且f(ek)≤0即可,
而g(e-1)=$\frac{3}{8}$e-2-2e-1+1>0,g(e-2)=$\frac{3}{8}$$\frac{1}{{e}^{4}}$-2$\frac{2}{{e}^{2}}$+2+lne-2=$\frac{1}{{e}^{2}}$($\frac{3}{8}$•$\frac{1}{{e}^{2}}$-2)<0,
当k≤-2且k∈z时均有g(ek)<0,即函数g(x)在[ek,e-1]?[ek,+∞)(k∈z)上有零点,
∴k的最大值为-2;
(Ⅲ)要证明f(x)≤1-$\frac{1}{x}$,即证$\frac{lnx}{x}$≤1-$\frac{1}{x}$(x>0),
只需证lnx-x+1≤0在(0,+∞)上恒成立,
令h(x)=lnx-x+1(x>0),由h′(x)=$\frac{1}{x}$-1=0得x=1,
则在x=1处h(x)有极大值(也是最大值),h(1)=0,
∴lnx-x+1≤0在(0,+∞)上恒成立,
因此f(n2)≤1-$\frac{1}{{n}^{2}}$,n∈N*,于是有:
f(22)+f(32)+…+f(n2)
≤(1-$\frac{1}{{2}^{2}}$)+(1-$\frac{1}{{3}^{2}}$)+…+(1-$\frac{1}{{n}^{2}}$)
=(n-1)-($\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$)
<(n-1)-[$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$]
=(n-1)-($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=(n-1)-($\frac{1}{2}$-$\frac{1}{n+1}$)=$\frac{(2n+1)(n-1)}{2(n+1)}$,
∴f(22)+f(32)+…+f(n2)<$\frac{(2n+1)(n-1)}{2(n+1)}$.
点评 本题考察了函数的单调性,考察导数的应用,不等式的证明问题,本题是一道难题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等腰或直角三角形 | ||
| C. | 等腰三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b | B. | a=b | ||
| C. | a>b | D. | a,b的大小与n的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 表示焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.
某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则图中a的值为0.005.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
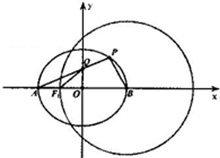 如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.
如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
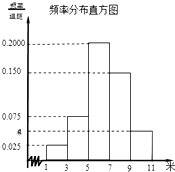 为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com