
分析 (Ⅰ)过A,B两点作准线的垂线,垂足分别为A1,B1,易知AF=AA1,BF=BB1,求出A,H的坐标,即可求直线AB的斜率;
(Ⅱ)若△ABF的面积为$\sqrt{2}$,可得${S_{△ABF}}={S_{△AHF}}=2{S_{△AHO}}=2×\frac{1}{2}|{OH}|•|{y_A}|=\frac{{\sqrt{2}}}{4}{p^2}$,即可求抛物线的方程.
解答 解:(Ⅰ)过A,B两点作准线的垂线,垂足分别为A1,B1,易知AF=AA1,BF=BB1,
∵|BF|=2|AF|,∴|BB1|=2|AA1|,∴A为HB的中点,又O是HF的中点,
∴AO是△BHF的中位线,∴$|{AO}|=\frac{1}{2}|{BF}|=|{AF}|$,而$F({\frac{p}{2},0})$,∴${x_A}=\frac{p}{4}$,
∴$y_A^2=2p•\frac{p}{4}=\frac{p^2}{2}$,${y_A}=±\frac{{\sqrt{2}}}{2}p$,∴$A({\frac{p}{4},±\frac{{\sqrt{2}p}}{2}})$,而$H({-\frac{p}{2},0})$
∴${k_{AB}}={k_{AH}}=\frac{{{y_H}-{y_A}}}{{{x_H}-{x_A}}}=±\frac{{2\sqrt{2}}}{3}$; …(6分)
(Ⅱ)∵A为HB的中点,O是HF的中点,
∴${S_{△ABF}}={S_{△AHF}}=2{S_{△AHO}}=2×\frac{1}{2}|{OH}|•|{y_A}|=\frac{{\sqrt{2}}}{4}{p^2}$,
∴$\frac{{\sqrt{2}}}{4}{p^2}=\sqrt{2}$,∴p=2,∴抛物线的方程为y2=4x. …(12分)
点评 本题考查抛物线的方程与性质,考查三角形中位线的性质,考查学生的计算能力,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
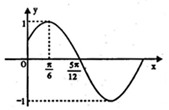 已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.
已知函数f(x)=Msin(ωx+φ)(M>0)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com