
在平面直角坐标系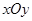 中,已知点
中,已知点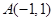 ,
,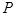 是动点,且
是动点,且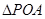 的三边所在直线的斜率满足
的三边所在直线的斜率满足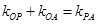 .
.
(1)求点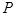 的轨迹
的轨迹 的方程;
的方程;
(2)若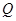 是轨迹
是轨迹 上异于点
上异于点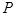 的一个点,且
的一个点,且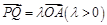 ,直线
,直线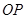 与
与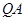 交于点
交于点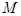 ,问:是否存在点
,问:是否存在点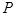 ,使得
,使得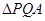 和
和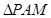 的面积满足
的面积满足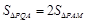 ?若存在,求出点
?若存在,求出点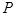 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)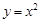 (
(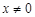 且
且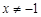 ),(2)
),(2)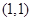
解析试题分析:(1)点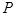 的轨迹的方程,就是找出点
的轨迹的方程,就是找出点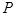 横坐标与纵坐标的关系式,而条件
横坐标与纵坐标的关系式,而条件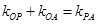 中只有点
中只有点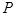 为未知,可直接利用斜率公式
为未知,可直接利用斜率公式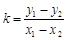 化简,得点
化简,得点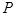 的轨迹的方程为
的轨迹的方程为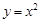 ,求出轨迹的方程后需结合变形过程及观察图像进行去杂,本题中分母不为零是限制条件,(2)本题难点在于对条件的转化,首先条件
,求出轨迹的方程后需结合变形过程及观察图像进行去杂,本题中分母不为零是限制条件,(2)本题难点在于对条件的转化,首先条件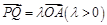 说明的是
说明的是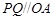 ,其次条件
,其次条件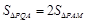 揭示的是
揭示的是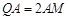 ,两者结合转化为条件
,两者结合转化为条件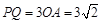 ,到此原题就转化为:已知斜率为
,到此原题就转化为:已知斜率为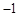 的过点
的过点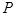 直线被抛物线
直线被抛物线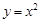 截得弦长为
截得弦长为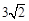 ,求点
,求点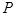 的坐标.
的坐标.
试题解析: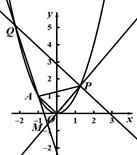
(1)设点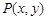 为所求轨迹上的任意一点,则由
为所求轨迹上的任意一点,则由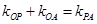 得,
得,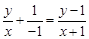 ,整理得轨迹
,整理得轨迹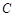 的方程为
的方程为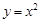 (
(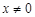 且
且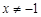 ). 3分
). 3分
(2):学设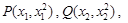 由
由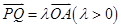 可知直线
可知直线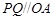 ,
,
则 ,故
,故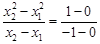 ,即
,即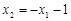 , 5分
, 5分
直线OP方程为: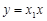 ①;直线QA的斜率为:
①;直线QA的斜率为: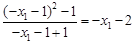 ,
,
∴直线QA方程为: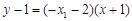 ,即
,即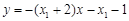 ②
②
联立①②,得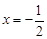 ,∴点M的横坐标为定值
,∴点M的横坐标为定值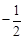 . 8分
. 8分
由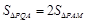 ,得到
,得到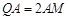 ,因为
,因为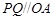 ,所以
,所以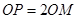 ,
,
由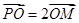 ,得
,得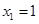 ,∴
,∴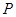 的坐标为
的坐标为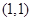 .
.
∴存在点P满足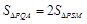 ,
,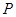 的坐标为
的坐标为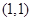 . 10分
. 10分
考点:轨迹方程,直线与抛物线位置关系


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
设椭圆M: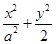 =1(a>
=1(a>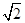 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x= 与x轴交于点A,若
与x轴交于点A,若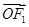 1=2
1=2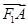 (其中O为坐标原点).
(其中O为坐标原点).
(1)求椭圆M的方程;
(2)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E,F为直径的两个端点),求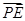 ·
·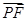 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于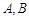 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,求
能否垂直?若能,求 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)已知点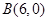 和
和 ,过点
,过点 的直线
的直线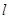 与过点
与过点 的直线
的直线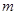 相交于点
相交于点 ,设直线
,设直线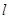 的斜率为
的斜率为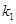 ,直线
,直线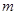 的斜率为
的斜率为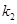 ,如果
,如果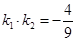 ,求点
,求点 的轨迹;
的轨迹;
(2)用正弦定理证明三角形外角平分线定理:如果在 中,
中,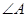 的外角平分线
的外角平分线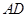 与边
与边 的延长线相交于点
的延长线相交于点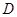 ,则
,则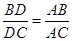 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系中,已知点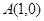 ,点
,点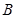 在直线
在直线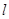 :
: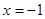 上运动,过点
上运动,过点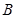 与
与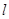 垂直的直线和线段
垂直的直线和线段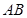 的垂直平分线相交于点
的垂直平分线相交于点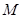 .
.
(1)求动点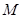 的轨迹
的轨迹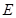 的方程;
的方程;
(2)过(1)中的轨迹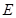 上的定点
上的定点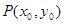
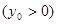 作两条直线分别与轨迹
作两条直线分别与轨迹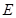 相交于
相交于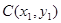 ,
,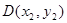 两点.试探究:当直线
两点.试探究:当直线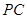 ,
,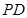 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线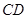 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆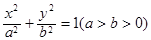 的左、右焦点分别为
的左、右焦点分别为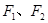 ,且
,且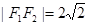 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线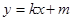 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点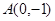 ,当
,当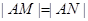 时,求实数m的取值范围,
时,求实数m的取值范围,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com