
分析 (Ⅰ)根据抛物线方程将A(1,1)代入,即可求得p的值,写出抛物线方程;
(Ⅱ)设出B和C点坐标及直线BC方程,代入抛物线方程,求得关于y的一元二次方程,求得y1+y2和y1y2的表达式,求得kAB•kAC=-1,即可求得m的值,写出直线BC方程,
即可证明恒过定点(2,-1).
解答 解:(Ⅰ)由题意得12=2p×1,
∴$p=\frac{1}{2}$,
∴所求抛物线的方程为y2=x.
(Ⅱ)证明:设B(x1,y1),C(x2,y2),BC:x=my+t,
由$\left\{\begin{array}{l}x=my+t\\{y^2}=x\end{array}\right.$得:y2-my-t=0,△>0,y1+y2=m,y1y2=-t,
由AB⊥AC,
kAB•kAC=$\frac{{y}_{1}-1}{{x}_{1}-1}$•$\frac{{y}_{2}-1}{{x}_{2}-1}$=$\frac{1}{{y}_{1}+1}$•$\frac{1}{{y}_{2}+1}$=-1,
∴y1•y2+y1+y2+1=-1,
∴-t+m=-2,
∴t=m+2,
∴BC:x=m(y+1)+2,
所以直线BC恒过定点(2,-1).
点评 本题考查了直线与抛物线的位置关系,证明直线AB必过定点时,要熟练掌握其中设而不求的解题思想,考查韦达定理的运用,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{9}{2}$ | C. | 4 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-3 | D. | 8-6$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 10π | B. | $\frac{26}{3}π$ | C. | $\frac{56}{3}π$ | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
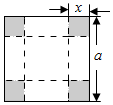 如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?
如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com