
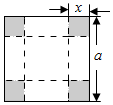
 如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?
如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大? 分析 设小正方形的边长为x,可得盒子高h=x,底边长为a-2x,可得盒子容积V=x(a-2x)2,(0<x<$\frac{a}{2}$),再由三元基本不等式,a+b+c≥3$\root{3}{abc}$,即可得到所求最大值.
解答 解:设小正方形的边长为x,
则盒子高h=x,底边长为a-2x,
得盒子容积V=x(a-2x)2,(0<x<$\frac{a}{2}$),
由V=$\frac{1}{4}$•4x•(a-2x)•(a-2x)≤$\frac{1}{4}$•($\frac{4x+a-2x+a-2x}{3}$)3
=$\frac{1}{4}$•$\frac{8{a}^{3}}{27}$=$\frac{2{a}^{3}}{27}$,
当且仅当4x=a-2x,即x=$\frac{a}{6}$∈(0,$\frac{a}{2}$),取得最大值.
故切去的正方形边长是$\frac{a}{6}$时,才能使盒子的容积最大.
点评 本题考查函数模型问题的解法,注意运用三元基本不等式求得最值,设出自变量求得函数的解析式是解题的关键,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{7}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x轴、y轴的正半轴于A、B两点,△AOB被圆分成四部分(如图),若这四部分图形的面积满足S1+S4=S2+S3,则直线AB有( )
过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x轴、y轴的正半轴于A、B两点,△AOB被圆分成四部分(如图),若这四部分图形的面积满足S1+S4=S2+S3,则直线AB有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 0条 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 三棱锥O-ABC中,M,N分别是AB,OC的中点,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{NM}$,则$\overrightarrow{NM}$等于( )
三棱锥O-ABC中,M,N分别是AB,OC的中点,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{NM}$,则$\overrightarrow{NM}$等于( )| A. | $\frac{1}{2}$(-$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) | B. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\frac{1}{2}$($\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$) | D. | $\frac{1}{2}$(-$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com