

分析 (1)根据茎叶图可知,鲤鱼与鲫鱼的平均数目分别为80,20.由题意知,求出池塘中鱼的总数目,由此能求出估计鲤鱼数目和鲫鱼数目.
(2)①根据题意,结合直方图能求出池塘中鱼的重量在3千克以上的条数.
②设第二组鱼的条数为x,则第三、四组鱼的条数分别为x+7、x+14,由此能求出第二、三、四组的频率分别为0.08、0.15、0.22,从而将频率分布直方图补充完整.
③由频率分布直方图能求出众数和平均数,从而得到鱼的总重量.
解答 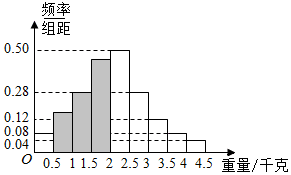 解:(1)根据茎叶图可知,鲤鱼与鲫鱼的平均数目分别为80,20.
解:(1)根据茎叶图可知,鲤鱼与鲫鱼的平均数目分别为80,20.
由题意知,池塘中鱼的总数目为1 000÷$\frac{80+20}{2000}$=20 000(条),
则估计鲤鱼数目为20 000×$\frac{80}{100}$=16 000(条)
鲫鱼数目为20 000-16 000=4 000(条).
(2)①根据题意,结合直方图可知,
池塘中鱼的重量在3千克以上(含3千克0的条数约为20 000×(0.12+0.08+0.04)×0.5=2 400(条).
②设第二组鱼的条数为x,则第三、四组鱼的条数分别为x+7,x+14,
则有x+x+7+x+14=100×(1-0.55),解得x=8,
故第二、三、四组的频率分别为0.08、0.15、0.22,
它们在频率分布直方图中的小矩形的高度分别为0.16,0.30,0.44,
据此可将频率分布直方图补充完整(如图).
③众数为2.25千克,
平均数为0.25×0.04+0.75×0.08+1.25×0.15+…+4.25×0.02=2.02(千克),
所以鱼的总重量为2.02×20 000=40 400(千克).
点评 本题考查频率分布直方图的应用,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{9}{2}$ | C. | 4 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 10π | B. | $\frac{26}{3}π$ | C. | $\frac{56}{3}π$ | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x-2y-3═0 | B. | x+2y-2═0 | C. | 4x+2y-3═0 | D. | x-2y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
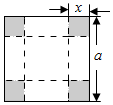 如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?
如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b | B. | a-b | C. | -a+b | D. | -a-b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com