Question

1．已知实数x，y满足x²+y²≤1，则|x+2y-2|+|6-2x-3y|的最大值是8+$\sqrt{34}$．

Answer 1

分析 根据题意，可得6-2x-3y＞0，直线x+2y-2=0将圆x²+y²=1分成两部分，
由此去掉绝对值|x+2y-2|+|6-2x-3y|，求出对应解析式的最大值即可．

解答 解：由x²+y²≤1，可得6-2x-3y＞0，即|6-2x-3y|=6-2x-3y，
如图所示，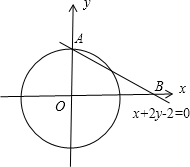
直线x+2y-2=0将圆x²+y²=1分成两部分，
在直线的上方（含直线），即有x+2y-2≥0，即|x+2y-2|=x+2y-2，
此时|x+2y-2|+|6-2x-3y|=（x+2y-2）+（6-2x-3y）=-x-y+4，
根据题意得在A（0，1）处取得最大值3；
在直线的下方（含直线），即有x+2y-2≤0，
即|x+2y-2|=-（x+2y-2），
此时|x+2y-2|+|6-2x-3y|=-（x+2y-2）+（6-2x-3y）=8-3x-5y，
设x=cosθ，y=sinθ，则
8-3x-5y=8-3cosθ-5sinθ=8-$\sqrt{{3}^{2}{+5}^{2}}$sin（θ+α）≤8+$\sqrt{34}$，sin（θ+α）=-1时取“=”；
综上，|x+2y-2|+|6-2x-3y|的最大值为8+$\sqrt{34}$．
故答案为：8+$\sqrt{34}$．

点评 本题考查了绝对值不等式的定义与应用问题，也考查了转化思想的应用问题，是综合性题目．