
 过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x轴、y轴的正半轴于A、B两点,△AOB被圆分成四部分(如图),若这四部分图形的面积满足S1+S4=S2+S3,则直线AB有( )
过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x轴、y轴的正半轴于A、B两点,△AOB被圆分成四部分(如图),若这四部分图形的面积满足S1+S4=S2+S3,则直线AB有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 0条 |
分析 设∠BAO=x,则x的范围可知,设f(x)=(S1+S4)-(S2+S3),根据图象可知那么x在增大的时候,f(x)递减;x接近0时f(x)>0;x接近$\frac{π}{2}$时f(x)<0,只有f(x)=0即S1+S4=S2+S3,进而可推断出在(0,$\frac{π}{2}$)上只有一个x使之成立,
解答 解:设∠BAO=x,则x∈(0,$\frac{π}{2}$),设f(x)=(S1+S4)-(S2+S3),
那么x在增大的时候(即直线AB顺时针旋转的过程中),
S1+S4递减,S2+S3递增,所以f(x)递减;
又x接近0时,S1+S4>S2+S3,所以f(x)>0;
x接近$\frac{π}{2}$时,S1+S4<S2+S3,所以f(x)<0,
所以f(x)=0即S1+S4=S2+S3,在(0,$\frac{π}{2}$)上只有一个x使之成立,
所以符合题意的直线AB有且只有一条
故选:A.
点评 本题主要考查了直线与圆相交的性质,考查了函数思想、数形结合思想的运用,考查了分析及推理能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | 10π | B. | $\frac{26}{3}π$ | C. | $\frac{56}{3}π$ | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
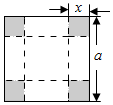 如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?
如图,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,问切去的正方形边长是多少时,才能使盒子的容积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 10 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b | B. | a-b | C. | -a+b | D. | -a-b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a=$\frac{1}{e}$”是“函数f(x)=logax在区间(0,+∞)上为减函数”的充分不必要条件 | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“x≠1,则x2-3x+2≠0” | |
| C. | 在回归分析中,求得的线性回归直线至少过一个样本点 | |
| D. | 若命题p:?n∈N,2n>1000,则非p:?n∈N,2n≤1000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com