
| A. | $y=-4sin(\frac{π}{8}x-\frac{π}{4})$ | B. | $y=4sin(\frac{π}{8}x-\frac{π}{4})$ | C. | $y=-4sin(\frac{π}{8}x+\frac{π}{4})$ | D. | $y=4sin(\frac{π}{8}x+\frac{π}{4})$ |
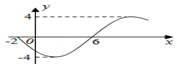
分析 观察函数的图象可得,函数的最小值-4,且在一周期内先出现最小值,所以A=-4,由图可得周期T=16,代入周期公式T=$\frac{2π}{ω}$可求ω;再把函数图象上的最值点代入结合已知φ的范围可得φ的值.
解答 解:由函数的图象可得最大值为4,且在一周期内先出现最小值,
所以A=-4
观察图象可得函数的周期T=16,ω=$\frac{2π}{16}$=$\frac{π}{8}$
又函数的图象过(2,-4)代入可得sin($\frac{π}{4}$+φ)=1
∴$\frac{π}{4}$+φ=$\frac{π}{2}$+2kπ
∵|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{4}$
∴函数的表达式y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$).
故选C.
点评 1本题主要考查了由三角函数的图象求解函数的解析式,其步骤一般是:由函数的最值求解A,(但要判断是先出现最大值或是最小值,从而判断A的正负号)由周期求解ω,由函数图象上的点(一般用最值点)代入求解φ.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线的一支 | B. | 椭圆 | ||
| C. | 双曲线的一支或椭圆 | D. | 双曲线或椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{27}$ | B. | $\frac{7}{81}$ | C. | $\frac{40}{243}$ | D. | $\frac{19}{144}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com