
 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.分析 (1)先求出A、B、P的坐标,从而求出直线AP的方程,进而求出弦AM的长;
(2)设出直线AP的方程,联立方程组,求出M点的坐标,结合BM⊥OP,求出a的值,从而求出曲线C的方程.
解答 解:(1)∵曲线C为圆,则曲线C为x2+y2=1,
∴A(-1,0),B(1,0),P(1,±$\frac{2\sqrt{3}}{3}$),
∴直线AP的方程为:y=±$\frac{\sqrt{3}}{3}$(x+1),
∴圆心到直线AP的距离为d=$\frac{1}{2}$,
∴弦AM=2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{1-\frac{1}{4}}$=$\sqrt{3}$;
(2)由已知得A(-a,0),B(a,0),
由于点N在以BP为直径的圆上,且O、N、P三点中线,故BM⊥OP,
显然,直线AP的斜率k存在且k≠0,可设直线AP的方程为y=k(x+a),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}{+y}^{2}=1}\\{y=k(x+a)}\end{array}\right.$得:(1+a2k2)x2+2a3k2x+a4k2-a2=0,
设点M(xM,yM),∴xM•(-a)=$\frac{{{a}^{4}k}^{2}{-a}^{2}}{1{{+a}^{2}k}^{2}}$,
故xM=$\frac{a{{-a}^{3}k}^{2}}{1{{+a}^{2}k}^{2}}$,从而yM=k(xM+a)=$\frac{2ak}{1{{+a}^{2}k}^{2}}$,
∴M($\frac{a{{-a}^{3}k}^{2}}{1{{+a}^{2}k}^{2}}$,$\frac{2ak}{1{{+a}^{2}k}^{2}}$),
∵B(a,0),∴$\overrightarrow{BM}$=($\frac{-{{2a}^{3}k}^{2}}{1{{+a}^{2}k}^{2}}$,$\frac{2ak}{1{{+a}^{2}k}^{2}}$),
由BM⊥OP,可得$\overrightarrow{BM}$•$\overrightarrow{OP}$=$\frac{-{{2a}^{4}k}^{2}+{{4a}^{2}k}^{2}}{1{{+a}^{2}k}^{2}}$=0,
即-2a4k2+4a2k2=0,
∵k≠0,a>0,∴a=$\sqrt{2}$,
经检验,当a=$\sqrt{2}$时,O、N、P三点共线,
∴曲线C的方程是:$\frac{{x}^{2}}{2}$+y2=1.
点评 本题考察了直线和圆锥曲线的问题,第一问中求出AP的方程是解题的关键,第二问中求出M点的坐标,利用向量垂直的性质是解题的关键,本题是一道难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.
如图在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进15m,至点C处测得顶端A的仰角为2θ,再继续前进5$\sqrt{3}$m至D点,测得顶端A的仰角为4θ,则建筑物AE的高为$\frac{15}{2}$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
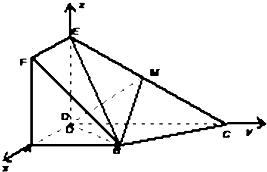 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com