

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
分析 由题意可得$\overrightarrow{A{B}_{2}}⊥\overrightarrow{{B}_{3}{C}_{3}}$,然后把mi=$\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}$转化为$\overrightarrow{A{B}_{2}}•\overrightarrow{A{C}_{3}}$求得答案.
解答 解:由图可知,∠B2AC3=30°,又∠AC3B3=60°,
∴$\overrightarrow{A{B}_{2}}⊥\overrightarrow{{B}_{3}{C}_{3}}$,即$\overrightarrow{A{B}_{2}}•\overrightarrow{{B}_{3}{C}_{3}}=0$.
则${m_i}=\overrightarrow{A{B_2}}•\overrightarrow{A{P_i}}=\overrightarrow{A{B_2}}(\overrightarrow{A{C_3}}+\overrightarrow{{C_3}{P_i}})=\overrightarrow{A{B_2}}•\overrightarrow{A{C_3}}=2\sqrt{3}×6×\frac{{\sqrt{3}}}{2}=18$,
∴m1+m2+…+m10=18×10=180.
故选:A.
点评 本题考查平面向量的数量积运算,考查了三角形中边角关系的运用,考查了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
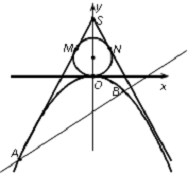 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 400 | B. | 500 | C. | 600 | D. | 800 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com