
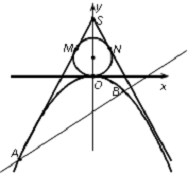
 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.分析 (1)1)设切线方程为y=kx+3,即 kx-y+3=0,圆心到直线的距离为d=1,求出k,可得切线方程,代入抛物线方程,利用△=0,求出抛物线的方程;
(2)设A(x1,y1),B(x2,y2).由|AF|=5,可得-y2+1=5,解得y2,代入抛物线方程可得x2.A,P,M三点共线,求出B的坐标,即可求出△BCF与△ACF的面积之比.
解答 解:(1)设切线方程为y=kx+3,即 kx-y+3=0,
圆Q:x2+y2-2y=0的圆心为(0,1),半径为1,圆心到直线的距离为d=$\frac{2}{\sqrt{{k}^{2}+1}}$=1,
∴k=$±\sqrt{3}$,
∴两切线的方程y=$±\sqrt{3}$x+3,
代入x2=-2py,可得x2±2$\sqrt{3}$px+6p=0,
△=12p2-24p=0,∴p=2,
∴抛物线C的方程x2=-4y;…(7分)
(2)设A(x1,y1),B(x2,y2).
由|AF|=5,可得-y2+1=5,
解得y2=-4,代入抛物线方程可得x2=-4.
∴A(-4,-4).
∵A,P,M三点共线,∴B(2,-1),
∴△BCF与△ACF的面积之比=$\frac{|BC|}{|AC|}$=$\frac{1+1}{4+1}$=$\frac{2}{5}$.
点评 本题考查了抛物线的定义及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
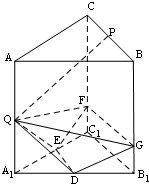 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | 5π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com