
分析 (1)根据三角函数的单调性即可求f(x)的单调增区间
(2)根据两角和差的正弦公式进行求解即可得到结论.
解答 解:(1)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,
得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,k∈Z,
即f(x)的单调增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)若$f(\frac{α}{2})=\frac{{\sqrt{2}}}{10}$,则sin(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,
若$α∈(\frac{π}{2},\frac{3π}{4})$,则α+$\frac{π}{4}$∈($\frac{3π}{4}$,π),
即cos(α+$\frac{π}{4}$)=-$\frac{7\sqrt{2}}{10}$,
则sinα=sin(α+$\frac{π}{4}$-$\frac{π}{4}$)=sin(α+$\frac{π}{4}$)cos$\frac{π}{4}$-cos(α+$\frac{π}{4}$)sin$\frac{π}{4}$
=$\frac{\sqrt{2}}{10}$×$\frac{\sqrt{2}}{2}$-(-$\frac{7\sqrt{2}}{10}$)×$\frac{\sqrt{2}}{2}$=$\frac{4}{5}$.
点评 本题主要考查三角函数单调区间的求解以及三角函数值的计算,利用两角和差的正弦公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
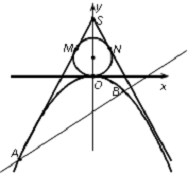 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [29.86, 29.90 ) | [29.90, 29.94) | [29.94, 29.98) | [29.9 8, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| p(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}{a^2}$ | B. | $-\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\frac{1}{2}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,sin2x≤1 | B. | ?x∉R,sin2x>1 | C. | ?x0∈R,sin2x≤1 | D. | ?x0∉R,sin2x>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,四边形ABCD的顶点都在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,对角线AC与BD分别过椭圆的左焦点F1(-1,0)和右焦点F2(1,0),且AC⊥BD,椭圆的一条准线方程为x=4.
如图,在平面直角坐标系xOy中,四边形ABCD的顶点都在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,对角线AC与BD分别过椭圆的左焦点F1(-1,0)和右焦点F2(1,0),且AC⊥BD,椭圆的一条准线方程为x=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com