
分析 (1)通过f(x)=f(1-x)=$\frac{1}{2}$,可得关系式ak+am-k=$\frac{1}{2}$,从而Sm=a1+a2+…+am-1+am=am-1+am-2+…+a1+am,计算即得结论;
(2)通过题意可知$\frac{1}{{1+b}_{n}}$=$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n+1}}$,从而Tn=3-$\frac{1}{{b}_{n+1}}$、数列{bn}是单调递增数列,利用T2≥T2,计算即得结论.
解答 解:(1)由题可知,f(x)=f(1-x)=$\frac{1}{2}$,
所以f($\frac{k}{m}$)+f(1-$\frac{k}{m}$)=$\frac{1}{2}$(1≤k≤m-1),
即f($\frac{k}{m}$)+f($\frac{m-k}{m}$)=$\frac{1}{2}$,∴ak+am-k=$\frac{1}{2}$,
由Sm=a1+a2+…+am-1+am ①
得Sm=am-1+am-2+…+a1+am ②
由①+②,得:2Sm=$\frac{1}{2}$(m-1)+2am=$\frac{m-1}{2}$+2×$\frac{1}{6}$=$\frac{m}{2}$-$\frac{1}{6}$,
∴Sm=$\frac{1}{12}$(3m-1);
(2)∵b1=$\frac{1}{3}$,bn+1=${{b}_{n}}^{2}$+bn=bn(bn+1),
∴对任意的m∈N+,bn>0,有:
$\frac{1}{{b}_{n+1}}$=$\frac{1}{{b}_{n}({b}_{n}+1)}$=$\frac{1}{{b}_{n}}$-$\frac{1}{{1+b}_{n}}$,即$\frac{1}{{1+b}_{n}}$=$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n+1}}$,
∴Tn=$\frac{1}{{b}_{1}}$-$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{2}}$-$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n+1}}$=$\frac{1}{{b}_{1}}$-$\frac{1}{{b}_{n+1}}$=3-$\frac{1}{{b}_{n+1}}$,
∵bn+1-bn=${{b}_{n}}^{2}$>0,∴数列{bn}是单调递增数列,
∴Tn关于n递增.当n≥2,且n∈N+时,Tn≥T2,
∵b1=$\frac{1}{3}$,b2=$\frac{1}{3}$($\frac{1}{3}$+1)=$\frac{4}{9}$,b3=$\frac{4}{9}$($\frac{4}{9}$+1)=$\frac{52}{81}$,
∴T2≥T2=3-$\frac{1}{{b}_{3}}$=$\frac{75}{52}$,
∴Sm<$\frac{75}{52}$,即$\frac{1}{12}$(3m-1)<$\frac{75}{52}$,
∴m<$\frac{238}{39}$=6$\frac{4}{39}$,∴m的最大值为6.
点评 本题考查求数列的递推关系及求和,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
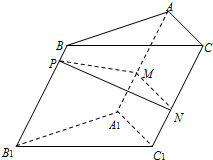 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.| 勾股定理的类比 | 三角形ABC | 四面体O-ABC |
| 条件 | AB⊥AC | OA、OB、OC两两垂直 |
| 结论 | AB2+AC2=BC2 | ? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 品牌 | 甲 | 乙 | |||
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 数量(件) | 2 | 3 | 45 | 5 | 45 |
| 每件利润(百元) | 1 | 2 | 3 | 1.8 | 2.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com