
| 分组 | [29.86, 29.90 ) | [29.90, 29.94) | [29.94, 29.98) | [29.9 8, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86, 29.90) | [29.90, 29.94) | [29.94, 29.98) | [29.98, 30.02) | [30.02, 30.06) | [30.06, 30.10) | [30.10, 30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | |||
| 非优质品 | |||
| 合计 |
| p(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析 (1)利用优质品数除以样本容量,即可估计零件的优质品率;
(2)利用统计数据可填写2×2列联表,再利用公式,求出k,利用给出的数据,即可得出结论.
解答 解:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为$\frac{360}{500}$=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为$\frac{320}{500}$=64%.
(2)
| 甲厂 | 乙厂 | 合计 | |
| 优质品 | 360 | 320 | 680 |
| 非优质品 | 140 | 180 | 320 |
| 合计 | 500 | 500 | 1000 |
点评 本题重点考查独立性检验的应用,解题的关键是正确统计,运用好公式,属于基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
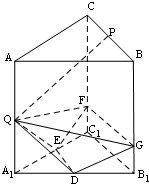 如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.
如图所示,正三棱柱ABC-A1B1C1中,P,Q,D,E分别是所在棱的中点,F,G是分别BB1,CC1上的点,满足$\frac{BG}{{G{B_1}}}=\frac{CF}{{F{C_1}}}$=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
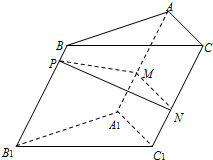 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.| 勾股定理的类比 | 三角形ABC | 四面体O-ABC |
| 条件 | AB⊥AC | OA、OB、OC两两垂直 |
| 结论 | AB2+AC2=BC2 | ? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 32 | C. | 60 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com