
分析 如图所示,设直线AB的方程为:ty=x-x0,A(x1,y1),B(x2,y2),与椭圆方程联立化为(4+t2)y2-2tx0y+x02-4=0.△>0.由于S△AOP=$\frac{1}{2}$|OP|•y1=y1,S△AOB=$\frac{1}{2}$x0|y1-y2|.S△AOB=2S△AOP,可得2y1=$\frac{1}{2}$x0|y1-y2|,再利用根与系数的关系可得:t2=$\frac{{{x}_{0}}^{4}-4{{x}_{0}}^{3}+16{x}_{0}-16}{4(1-{x}_{0})}$.令m=x0,f(m)=m4-4m3+16m-16,(m∈(0,2)),利用导数研究其单调性即可得出.
解答 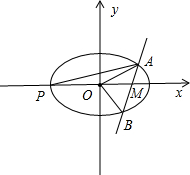 解:如图所示,
解:如图所示,
设直线AB的方程为:ty=x-x0,A(x1,y1),B(x2,y2),
(y1>y2,y1>0).
联立 $\left\{\begin{array}{l}{ty=x-{x}_{0}}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
化为(4+t2)y2-2tx0y+x02-4=0.
∴△=4t2x02-4(4+t2)(x02-4)>0,
∴y1+y2=$\frac{2t{x}_{0}}{4+{t}^{2}}$,①
y1y2=$\frac{{{x}_{0}}^{2}-4}{4+{t}^{2}}$,②
S△AOP=$\frac{1}{2}$|OP|•y1=y1,S△AOB=$\frac{1}{2}$x0|y1-y2|.
∵S△AOB=2S△AOP,
∴2y1=$\frac{1}{2}$x0|y1-y2|.
化为y2=(1-$\frac{4}{{x}_{0}}$)y1,代入①可得:y1=$\frac{2t{{x}_{0}}^{2}}{(2{x}_{0}-4)(4+{t}^{2})}$,
∴y2=$\frac{2t{x}_{0}({x}_{0}-4)}{(2{x}_{0}-4)(4+{t}^{2})}$,
∴$\frac{2t{{x}_{0}}^{2}}{(2{x}_{0}-4)(4+{t}^{2})}$•$\frac{2t{x}_{0}({x}_{0}-4)}{(2{x}_{0}-4)(4+{t}^{2})}$=$\frac{{{x}_{0}}^{2}-4}{4+{t}^{2}}$,
化为t2=$\frac{{{x}_{0}}^{4}-4{{x}_{0}}^{3}+16{x}_{0}-16}{4(1-{x}_{0})}$.(*)
令m=x0,f(m)=m4-4m3+16m-16,(m∈(0,2)),
f′(m)=4m3-12m2+16=4(m-2)2(m+1),
∴函数f(m)在m∈(0,2)单调递增,
又f(0)=-16,f(1)=-3,f(2)=0,
因此要使(*)有解,则1<m<2,
即x0∈(1,2).
故答案为:(1,2).
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、三角形面积计算公式、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
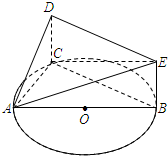 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
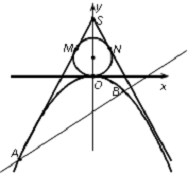 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com