
| A. | 6π | B. | 5π | C. | 4π | D. | 2π |
分析 由偶函数的定义域关于原点对称求出a的值,由偶函数的定义f(x)=f(-x),求出b的值,将a,b代入函数$y=2cos[(a+b)x-\frac{π}{3}]$,求出ω,从而求出最小正周期.
解答 解:∵函数f(x)=ax2+bx+3a+b是定义在[a-1,2a]的偶函数,
∴a-1+2a=0,解得a=$\frac{1}{3}$,
由f(x)=f(-x)得,b=0,
∴$y=2cos[(a+b)x-\frac{π}{3}]$=2cos($\frac{1}{3}$x-$\frac{π}{3}$),
∴T=$\frac{2π}{ω}$=6π,
故选:A.
点评 本题考查了偶函数定义的应用,考察三角函数问题,利用奇(偶)函数的定义域一定关于原点对称,这是容易忽视的地方.


科目:高中数学 来源: 题型:解答题
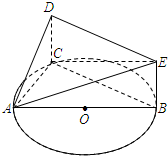 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
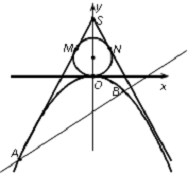 如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.
如图所示,已知点S(0,3),过点S作直线SM,SN与圆Q:x2+y2-2y=0和抛物线C:x2=-2py(p>0)都相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 400 | B. | 500 | C. | 600 | D. | 800 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}{a^2}$ | B. | $-\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\frac{1}{2}{a^2}$ | D. | $\frac{{\sqrt{3}}}{2}{a^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com