
分析 (Ⅰ)利用矩阵的运算法则进行求解;(Ⅱ)利用矩阵的乘法法则进行求解.
解答 解:(Ⅰ)设M=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$
则$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{2}\\{3}\end{array}]$=4$[\begin{array}{l}{2}\\{3}\end{array}]$=$[\begin{array}{l}{8}\\{12}\end{array}]$,∴$\left\{\begin{array}{l}{2a+3b=8}\\{2c+3d=12}\end{array}\right.$①
又$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{1}\\{-1}\end{array}]$=(-1)$[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{-1}\\{1}\end{array}]$,∴$\left\{\begin{array}{l}{a-b=-1}\\{c-d=1}\end{array}\right.$②
由①②可得a=1,b=2,c=3,d=2,∴M=$[\begin{array}{l}{1}&{2}\\{3}&{2}\end{array}]$;
(Ⅱ)易知$\overrightarrow{α}$=0•$[\begin{array}{l}{2}\\{3}\end{array}]$+(-1)$[\begin{array}{l}{1}\\{-1}\end{array}]$,
∴M5$\overrightarrow{α}$=(-1)6$\overrightarrow{α}$=$[\begin{array}{l}{-1}\\{1}\end{array}]$.
点评 本题考查矩阵的运算法则,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:解答题
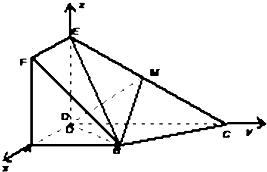 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6π | B. | 5π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 180 | B. | $60\sqrt{3}$ | C. | 45 | D. | $15\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
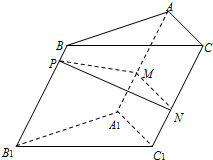 如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.| 勾股定理的类比 | 三角形ABC | 四面体O-ABC |
| 条件 | AB⊥AC | OA、OB、OC两两垂直 |
| 结论 | AB2+AC2=BC2 | ? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com