
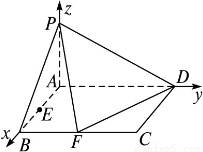
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
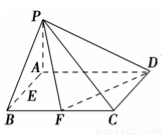
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
(1)详见解析;(2)详见解析;(3)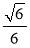 .
.
【解析】
试题分析:解法一(向量法)
(I)建立如图所示的空间直角坐标系A-xyz,分别求出直线PF与FD的平行向量,然后根据两个向量的数量积为0,得到PF⊥FD;
(2)求出平面PFD的法向量(含参数t),及EG的方向向量,进而根据线面平行,则两个垂直数量积为0,构造方程求出t值,得到G点位置;
(3)由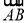 是平面PAD的法向量,根据PB与平面ABCD所成的角为45°,求出平面PFD的法向量,代入向量夹角公式,可得答案.
是平面PAD的法向量,根据PB与平面ABCD所成的角为45°,求出平面PFD的法向量,代入向量夹角公式,可得答案.
解法二(几何法)
(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,再由线面垂直的性质定理得到PF⊥FD;
(2)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有AH=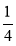 AD,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
AD,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=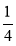 AP,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;
AP,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;
(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB与平面ABCD所成的角,即∠PBA=45°,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A-PD-F的平面角,解三角形MNF可得答案..
试题解析:(1)证明:∵PA⊥平面ABCD,∠BAD=90°,AB=1,AD=2,建立如图所示的空间直角坐标系A-xyz,则
A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).
不妨令P(0,0,t),∵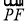 =(1,1,-t),
=(1,1,-t),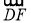 =(1,-1,0),
=(1,-1,0),
∴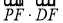 =1×1+1×(-1)+(-t)×0=0,
=1×1+1×(-1)+(-t)×0=0,
即PF⊥FD.
(2)【解析】
设平面PFD的法向量为n=(x,y,z),
由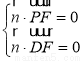 得
得
令z=1,解得:x=y= .
.
∴n= .
.
设G点坐标为(0,0,m),E ,则
,则 ,
,
要使EG∥平面PFD,只需 ·n=0,即
·n=0,即 ,得m=
,得m=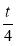 ,从而满足AG=
,从而满足AG=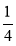 AP的点G即为所求.
AP的点G即为所求.
(3)【解析】
∵AB⊥平面PAD,∴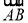 是平面PAD的法向量,易得
是平面PAD的法向量,易得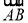 =(1,0,0),又∵PA⊥平面ABCD,∴∠PBA是PB与平面ABCD所成的角,得∠PBA=45°,PA=1,平面PFD的法向量为n=
=(1,0,0),又∵PA⊥平面ABCD,∴∠PBA是PB与平面ABCD所成的角,得∠PBA=45°,PA=1,平面PFD的法向量为n=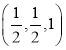 .
.
∴ .
.
故所求二面角A-PD-F的余弦值为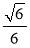 .
.
考点:1.用空间向量求平面间的夹角;2.空间中直线与直线之间的位置关系;3.直线与平面平行的判定.


科目:高中数学 来源:2015届浙江省高二下学期期中文科数学试卷(解析版) 题型:选择题
已知命题p:若x>0且y>0,则xy>0,则p的否命题是( )
A.若x>0且y>0,则xy≤0
B.若x≤0且y≤0,则xy≤0
C.若x,y至少有一个不大于0,则xy<0
D.若x,y至少有一个小于或等于0,则xy≤0
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期期中文科数学试卷(解析版) 题型:选择题
已知命题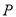 :函数
:函数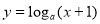 在
在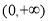 内单调递减;
内单调递减;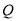 :曲线
:曲线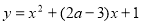 与
与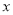 轴没有交点.如果“
轴没有交点.如果“ 或
或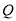 ”是真命题,“
”是真命题,“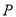 且
且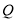 ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
A.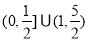 B.
B.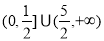
C. D.
D.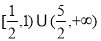
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设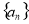 是首项为
是首项为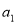 ,公差为
,公差为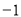 的等差数列,
的等差数列, 为其前n项和,若
为其前n项和,若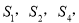 成等比数列,则
成等比数列,则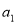 =( )
=( )
A.2 B.-2 C. D .
D .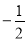
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期第一次统练理科数学试卷(解析版) 题型:选择题
对于曲线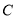 ∶
∶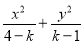 =1,给出下面四个命题:
=1,给出下面四个命题:
(1)曲线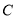 不可能表示椭圆;
不可能表示椭圆;
(2)若曲线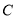 表示焦点在x轴上的椭圆,则1<
表示焦点在x轴上的椭圆,则1<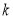 <
<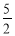 ;
;
(3)若曲线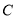 表示双曲线,则
表示双曲线,则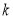 <1或
<1或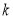 >4;
>4;
(4)当1<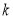 <4时曲线
<4时曲线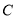 表示椭圆,其中正确的是 ( )
表示椭圆,其中正确的是 ( )
A .(2)(3) B. (1)(3) C. (2)(4) D.(3)(4)
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高三上学期第一次统练文科数学试卷(解析版) 题型:填空题
数列 是公比为
是公比为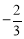 的等比数列,
的等比数列, 是首项为12的等差数列.现已知a9>b9
是首项为12的等差数列.现已知a9>b9
且a10>b10,则以下结论中一定成立的是 .(请填写所有正确选项的序号)
①  ; ②
; ②  ; ③
; ③ 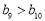 ; ④
; ④ 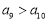 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com