
在正项等比数列{an}中,an+1<an,a2·a8=6,a4+a6=5,则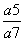 =( )
=( )
A.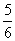 B.
B.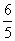 C.
C.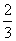 D.
D.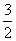
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
某体育用品商场经营一批每件进价为40元的运动服,先做了市场调查,得到数据如下表:
| 销售单价x(元) | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y(件) | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据,解答下列问题:
⑴ 建立一个恰当的函数模型,使它能较好地反映销售量y(件)与销售单价x(元)之间的函数关系,并写出这个函数模型的解析式 ;
;
⑵ 试求销售利润z(元)与销售单价x(元)之间的函数关系式(销售利润 = 总销售收入 - 总进价成本)并求价格为多少利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
如果对定义在R上的函数f(x),以任意两个不相等的实数x1,x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1),则称函数f(x)为“H函数”.给出下列函数:①y=-x3+x+1;②y=3x-2(sin x-cos x);③y=ex+1;④f(x)=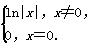 以上函数是“H函数”的所有序号为________.
以上函数是“H函数”的所有序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在等差数列{an}中,a1=-2 012,其前n项和为Sn,若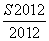 -
- =2 002,则S2 014的值等于( )
=2 002,则S2 014的值等于( )
A.2 011 B.-2 012
C.2 014 D.-2 013
查看答案和解析>>
科目:高中数学 来源: 题型:
在等比数列{an}中,a1=2,且an+1=an+2n.
(1)求数列{an}的通项an;
(2)数列{an}中是否存在这样的两项ap,aq(p<q),使得ap+aq=2 014?若存在,求符合条件的所有的p,q;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}(n=1,2,3,…,2 012),圆C1:x2+y2-4x-4y=0和圆C2:x2+y2-2anx-2a2 013-ny=0,若圆C2平分圆C1的周长,则{an}的所有项的和为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com