
分析 作出f(x)的函数图象,判断a,b,c的关系和范围,从而得出答案.
解答 解:f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{lo{g}_{2017}\frac{x}{π},x>π}\end{array}\right.$,
作出f(x)的函数图象如图所示: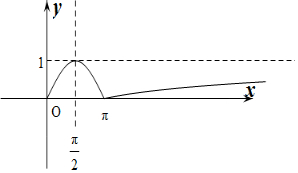
∵存在三个不相等的实数a,b,c使得f(a)=f(b)=f(c),不妨设a<b<c,
则0$<a<\frac{π}{2}$,$\frac{π}{2}<b<π$,
令log2017$\frac{x}{π}$=1得x=2017π,∴π<c<2017π,
∵f(x)在[0,π]上的图象关于直线x=$\frac{π}{2}$对称,∴a+b=π,
∴a+b+c∈(2π,2018π).
故答案为(2π,2018π).
点评 本题考查了方程解与函数图象的关系,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{49}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(1,+∞),x3+16≤8x | B. | ?x∈(1,+∞),x3+16<8x | ||
| C. | ?x∈(1,+∞),x3+16≤8x | D. | ?x∈(1,+∞),x3+16<8x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
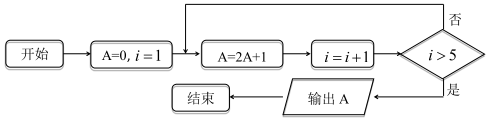
| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,6] | B. | [5,7] | C. | [4,6] | D. | [6,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {d} | C. | {a,c} | D. | {b,e} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com