
���� ��������ԲC�ı�����Ϊ$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0�����������ʹ�ʽ��a��b��c�Ĺ�ϵ�����a��b�����ɵõ���Բ���̣�
����i����M��x1��y1����N��x2��y2��������ֱ�ߵ�б�ʹ�ʽ�������ֱ��MN��y=kx+t��������Բ���̣��ɵã�3+k2��x2+2ktx+t2-3=0������Τ�ﶨ�������M��N��ֱ���ϣ�����ֱ�߷��̣������������ɵ�t�ķ��̣��ⷽ�̿ɵ�t������֤��ֱ��MN������㣻
��ii���ɣ�i���ɵ�$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2�����ã�i���Ľ��ۣ����б�ʽ����0�����������������û�Ԫ�����ɲ���ʽ�����ʣ����ɵõ�����Χ��
��� �⣺��������ԲC�ı�����Ϊ$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0����
������ɵ�a2-b2=2��e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$��c=$\sqrt{2}$��
���a=$\sqrt{3}$��b=1��
������Բ�ı�����Ϊ$\frac{{y}^{2}}{3}$+x2=1��
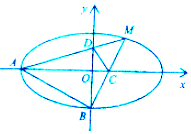
����i��֤������M��x1��y1����N��x2��y2����
��A��0��-$\sqrt{3}$����ֱ��AM��AN��б��֮��Ϊ1��
�ɵ�$\frac{{y}_{1}+\sqrt{3}}{{x}_{1}}$•$\frac{{y}_{2}+\sqrt{3}}{{x}_{2}}$=1��
����x1x2=y1y2+$\sqrt{3}$��y1+y2��+3��
�������ֱ֪��MN��б�ʴ����Ҳ�Ϊ0����ֱ��MN��y=kx+t��
������Բ���̣��ɵã�3+k2��x2+2ktx+t2-3=0��
�ɵ�x1x2=$\frac{{t}^{2}-3}{3+{k}^{2}}$��x1+x2=-$\frac{2kt}{3+{k}^{2}}$��
y1+y2=k��x1+x2��+2t=2t-$\frac{2{k}^{2}t}{3+{k}^{2}}$=$\frac{6t}{3+{k}^{2}}$��
y1y2=k2x1x2+kt��x1+x2��+t2=k2•$\frac{{t}^{2}-3}{3+{k}^{2}}$+kt��-$\frac{2kt}{3+{k}^{2}}$��+t2=$\frac{3{t}^{2}-3{k}^{2}}{3+{k}^{2}}$��
��$\frac{{t}^{2}-3}{3+{k}^{2}}$=$\frac{3{t}^{2}-3{k}^{2}}{3+{k}^{2}}$+$\sqrt{3}$��$\frac{6t}{3+{k}^{2}}$��+3��
��Ϊt2+3$\sqrt{3}$t+6=0��
���t=-2$\sqrt{3}$��-$\sqrt{3}$��ȥ����
��ֱ��MN�ķ���Ϊy=kx-2$\sqrt{3}$��
��ֱ��MN������㣬�ö�������Ϊ��0��-2$\sqrt{3}$����
��ii���ɣ�i���ɵ�$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2
=$\frac{{t}^{2}-3}{3+{k}^{2}}$+$\frac{3{t}^{2}-3{k}^{2}}{3+{k}^{2}}$=$\frac{4{t}^{2}-3-3{k}^{2}}{3+{k}^{2}}$=$\frac{45-3{k}^{2}}{3+{k}^{2}}$��
�ɣ�3+k2��x2+2ktx+t2-3=0��
�ɵá�=4k2t2-4��t2-3����3+k2��=48k2-36��3+k2����0��
���k2��9��
��3+k2=m����m��12����k2=m-3��
����$\frac{45-3{k}^{2}}{3+{k}^{2}}$=$\frac{45-3��m-3��}{m}$=$\frac{54}{m}$-3��
��m��12���ɵ�-3��$\frac{54}{m}$-3��$\frac{3}{2}$��
��$\overrightarrow{OM}$•$\overrightarrow{ON}$��ȡֵ��Χ�ǣ�-3��$\frac{3}{2}$����
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ������ֱ�ߺ���������⣬ע������ֱ�߷��̺���Բ���̣�����Τ�ﶨ�����б�ʽ����0���Լ�ֱ�ߵ�б�ʹ�ʽ�������������������ʾ������ת��˼��ͻ�����������������������һ�����ۺ��ԣ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ��������DZ�Ƭ����Գ�����ˮ�洹ֱ�����ٵ�����ˮ�棬��tʱʱ�������¶��ˮ�沿�ֵ�ͼ�����ΪS��t����S��0��=0��������y=S�䣨t����ͼ�����Ϊ��������
��ͼ��һ��������DZ�Ƭ����Գ�����ˮ�洹ֱ�����ٵ�����ˮ�棬��tʱʱ�������¶��ˮ�沿�ֵ�ͼ�����ΪS��t����S��0��=0��������y=S�䣨t����ͼ�����Ϊ��������| A�� | 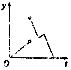 | B�� | 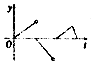 | C�� | 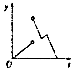 | D�� | 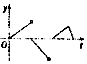 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $a��\frac{2}{3}$ | B�� | a��0 | C�� | $0��a��\frac{2}{3}$ | D�� | a��0��$a��\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{6}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{3}}}{2}$������Բ�Ľ������볤�ᴹֱ���ҳ�Ϊ1��
��֪��Բ$C��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{3}}}{2}$������Բ�Ľ������볤�ᴹֱ���ҳ�Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�e4�� | B�� | ��e4��+�ޣ� | C�� | ��-�ޣ�0�� | D�� | ��0��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com